Activité 1 – L’estimation de la biodiversité sur Terre Corrigé

« Activité 1 – L’estimation de la biodiversité sur Terre Corrigé : 1 - On observe que la diversité spécifique dans le site Avaro 37 est beaucoup plus faible (7 espèces) que dans le site Avaro 70 (22 espèces).

Le site Avaro 70 a une orientation sud, ce qui entraîne une fonte des neiges plus tôt que dans le site Avaro 37.

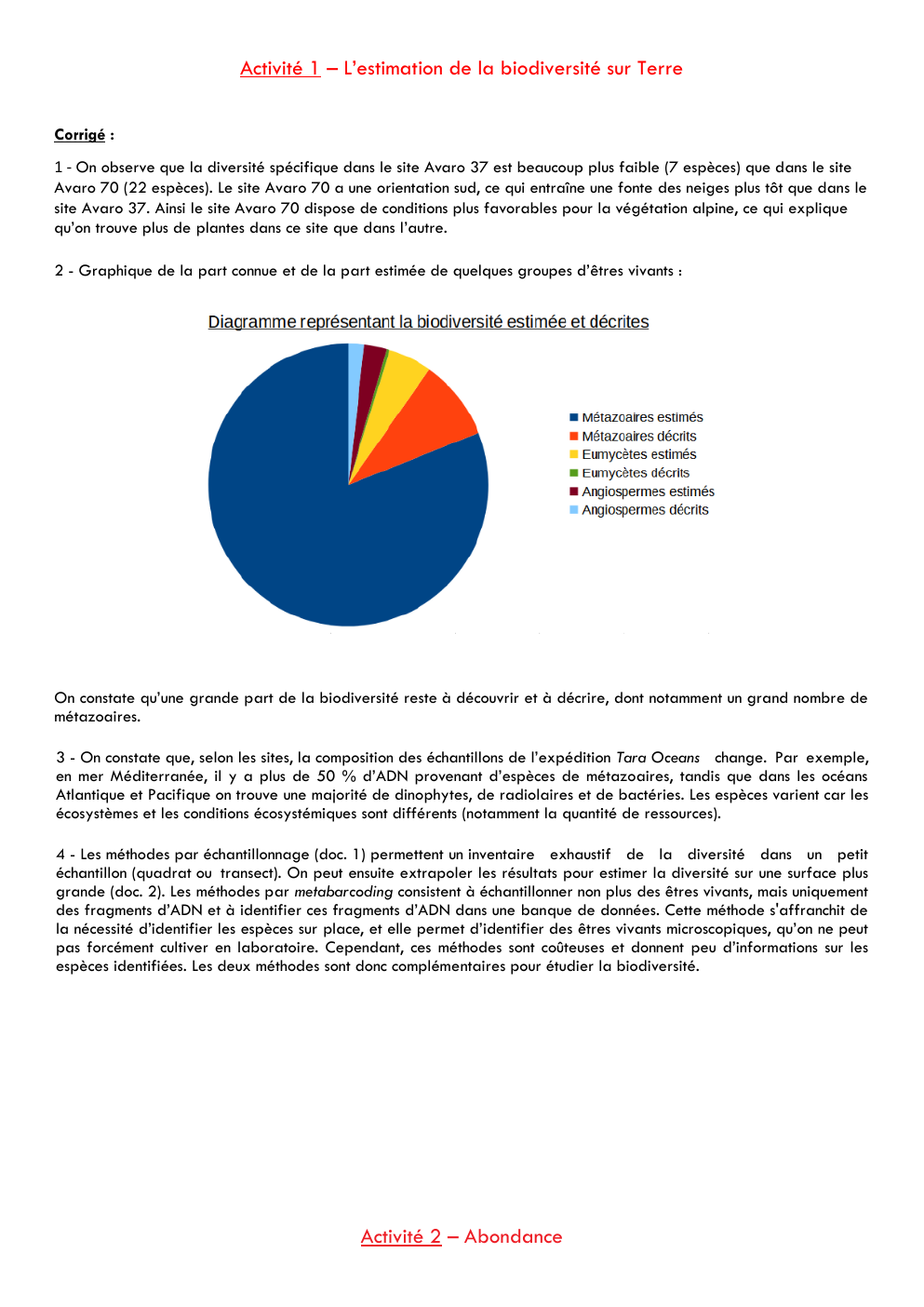
Ainsi le site Avaro 70 dispose de conditions plus favorables pour la végétation alpine, ce qui explique qu’on trouve plus de plantes dans ce site que dans l’autre. 2 - Graphique de la part connue et de la part estimée de quelques groupes d’êtres vivants : On constate qu’une grande part de la biodiversité reste à découvrir et à décrire, dont notamment un grand nombre de métazoaires. 3 - On constate que, selon les sites, la composition des échantillons de l’expédition Tara Oceans change.

Par exemple, en mer Méditerranée, il y a plus de 50 % d’ADN provenant d’espèces de métazoaires, tandis que dans les océans Atlantique et Pacifique on trouve une majorité de dinophytes, de radiolaires et de bactéries.

Les espèces varient car les écosystèmes et les conditions écosystémiques sont différents (notamment la quantité de ressources). 4 - Les méthodes par échantillonnage (doc.

1) permettent un inventaire exhaustif de la diversité dans un petit échantillon (quadrat ou transect).

On peut ensuite extrapoler les résultats pour estimer la diversité sur une surface plus grande (doc.

2).

Les méthodes par metabarcoding consistent à échantillonner non plus des êtres vivants, mais uniquement des fragments d’ADN et à identifier ces fragments d’ADN dans une banque de données.

Cette méthode s'affranchit de la nécessité d’identifier les espèces sur place, et elle permet d’identifier des êtres vivants microscopiques, qu’on ne peut pas forcément cultiver en laboratoire.

Cependant, ces méthodes sont coûteuses et donnent peu d’informations sur les espèces identifiées.

Les deux méthodes sont donc complémentaires pour étudier la biodiversité. Activité 2 – Abondance Corrigé : 1 - D’après le doc.

1, On en déduit donc que Le P est retiré car on part du principe que la population ne se modifie pas entre les deux échantillonnage → proportion d’individu marque reste la même. 2Recapture 1 2 3 4 (1291 x 1107) / 363 N 3 565,9 4 180,4 3 937 4 458,8 3 - L’estimation moyenne de l’abondance des jeunes otaries est de 4 035,5 jeunes otaries.

Si on compare les mesures obtenues on a jusqu’à environ 800 otaries d’écart (mesures 1 et 4).

Il est donc important de répéter si possible les échantillonnages afin d’avoir l’estimation la plus précise possible. 4 - Entre 1991 et 1998 la population d’otaries à fourrure a augmenté (plus de jeunes). Activité 3 – La proportion Corrigé : 1 - On remarque dans les photographies que selon la couleur et la luminosité des récifs les poissons clairs et sombres sont plus ou moins bien camouflés.

Dans la photographie a, on ne voit presque pas l’épervier foncé et, dans la photographie b, c’est l’épervier clair qui est invisible.

On peut supposer que la couleur des récifs varie en fonction de la profondeur. Ainsi, à faible profondeur, les récifs sont plutôt sombres et les poissons sombres sont mieux camouflés face aux prédateurs. À l’inverse, dans les eaux profondes, les coraux sont plus clairs et les poissons clairs sont camouflés. On peut supposer que la différence de couleur des poissons est due à une prédation différentielle des poissons clairs ou sombres selon la couleur des récifs.

On peut aussi supposer une évolution locale, à condition qu’il y ait peu d’échanges génétiques entre les poissons des eaux superficielles et les poissons des eaux profondes. 2- Eaux superficielles Eaux profondes n (population totale) f* 848 0,63 258 0,08 Borne inférieure de Borne supérieure de l’intervalle de confiance* l’intervalle de confiance* 0,6 0,05 0,66 0,11 * = voir formules livre doc.

2 p.

175 3 - L’intervalle de confiance est inversement proportionnel à la racine de la taille de l’échantillon.

Ainsi, plus la taille de l’échantillon sera grande plus la valeur de réduit. sera petite et donc plus l’intervalle de confiance est Cependant, pour des échantillons suffisamment grands, la différence sur l’intervalle de confiance est faible.

Par exemple, pour n = 848 on obtient une valeur de f de ± 0,032 alors que pour n = 258 la valeur de f est ± 0,033 donc une différence de 0,001 ! Activité 4 – La composante génétique Corrigé : 1 – Fréquence de A : Fréquence de a : 2 – (On peut préciser aux élèves qu’il s’agit de prédire les fréquences des génotypes à la génération 2.) En admettant que la population est assez grande et que la reproduction se fait au hasard, la probabilité de transmettre un allèle A est sa fréquence p. À la génération 1, la fréquence de A est À la génération 1, la fréquence de a est (cf.

doc.

4). . On peut réaliser le tableau de croisement suivant pour la génération 2 : On peut donc prédire que les génotypes à la génération suivante seront : 3 – D’après la question 1 on sait que p = 0,25 et q = 0,75. 4 – (On cherche ici, à retrouver f(A//A) = p² quelque soit la génération.) D’après les calculs (question 3) et le doc.

3, on constate que : On constate qu’à partir de la génération 2, les fréquences des allèles (p et q), ainsi que les fréquences des génotypes (p2, 2pq, q2), restent stables. Si à la génération N on a : On peut en déduire la fréquence des génotypes à la génération N+1 : = (fréquence de A à la génération N)2 Le raisonnement est le même pour la fréquence de a//a.

Ainsi, au cours des générations, la fréquence des génotypes ne change pas : on peut parler d’équilibre. 5 – En comparant les fréquences attendues (question 3) et les fréquences observées (document 1), on constate que les fréquences observées ne suivent pas l’équilibre de Hardy-Weinberg, avec notamment un excès de loups hétérozygotes A//a et un déficit de loups homozygotes.... »