Mouvements rectilignes et parabolique dans un champ de pesanteur uniforme

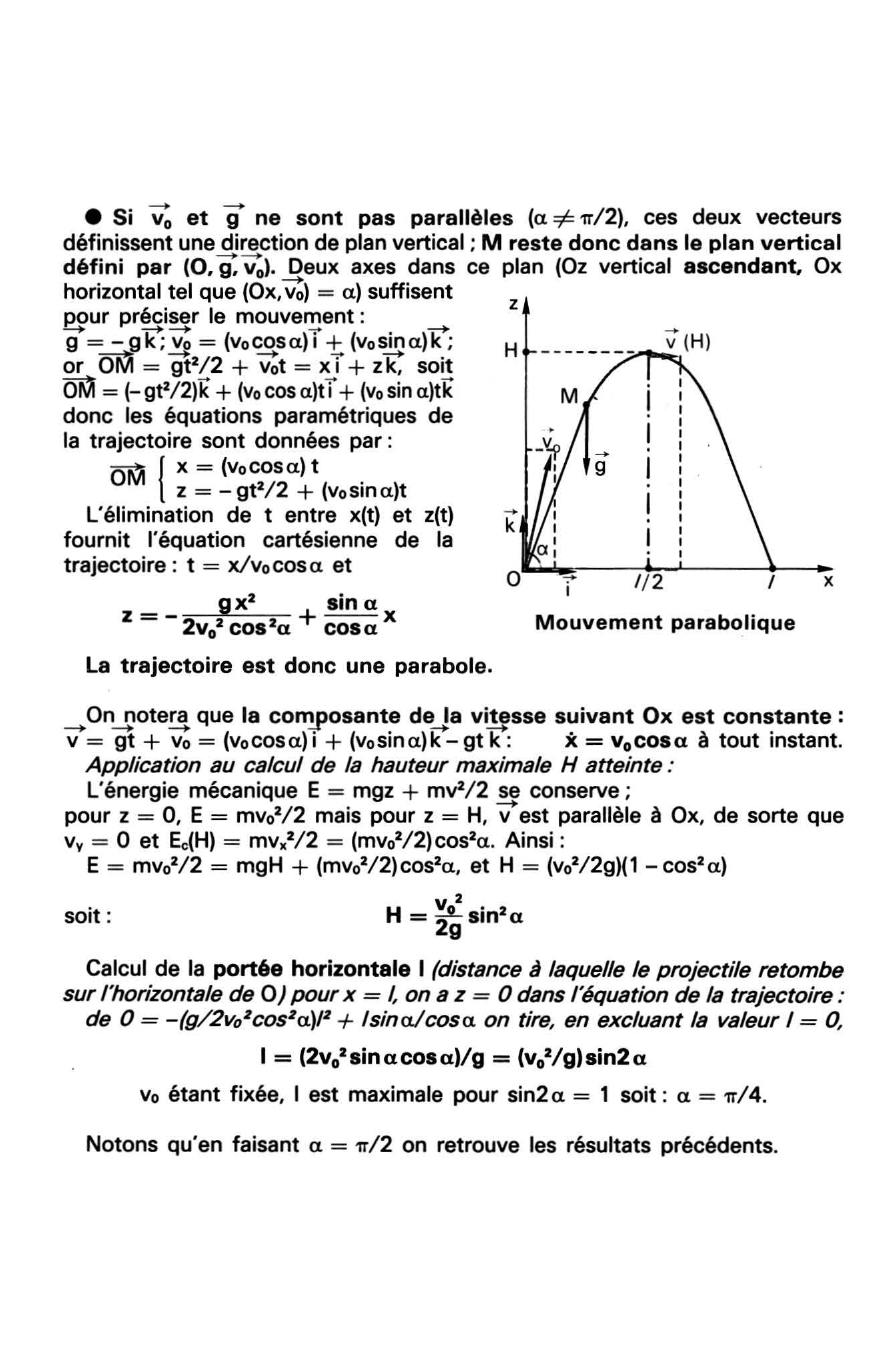
« e Si "V; et g ne sont pas parallèles (a =1= 1r/2), ces deux vecteurs définissent une direction de plan vertical ; M reste donc dans le plan vertical défini par (0, Q."V;).

Deux axes dans ce plan (Oz vertical ascendant, Ox horizontal tel que (Ox.~) = a) suffisent pour préciser le mouvement : g = -gk;~ = (vocosa)T + (vosina)k; or DM= gt2/2 + ~t = xT + z""it soit ~ = (-gt 2/2)k + (vocosa)tT + (vosina)tk donc les équations paramétriques de la trajectoire sont données par : ~ { X= (VoCOSa) t z =- gt2/2 + (vosina)t L'élimination de t entre x(t) et z(t) fournit l'équation cartésienne de la trajectoire: t = x/vocosa et z-- gx• sinax - 2v02 cos•a +cos a La trajectoire est donc une parabole.

z H · -i 1 / 2 x Mouvement parabolique -.

On~ote~ que la com_J>osant~ deja v~sse s~ivant Ox est con~tante : v = gt + Vo = (vocosa) 1 + (voslna)k- gt k: x= v0cosa à tout Instant.

Application au calcul de la hauteur maximale H atteinte : L'énergie mécanique E = mgz + mv 2/2 se conserve; pour z = 0, E = mvo 2/2 mais pour z = H, v est parallèle à Ox, de sorte que Vv = 0 et Ec(H) = mvl/2 = (mvo 2/2)cos 2a.

Ainsi: E = mvo 2/2 = mgH + (mvo 2/2)cos 2a, et H = (vo2/2g)(1- cos 2a) soit : v• H =~sin 2a Calcul de la portée horizontale 1 (distance à laquelle le projectile retombe sur l'horizontale de 0) pour x = /, on a z = 0 dans l'équation de la trajectoire : de 0 = -(g/2vozcosza)lz + lsinalcosa on tire, en excluant la valeur 1 = 0, 1 = (2v 02sinacosa)/g = (v0 2/g)sin2a vo étant fixée, 1 est maximale pour sin2a = 1 soit: a = 1T/4.

Notons qu'en faisant a= 1r/2 on retrouve les résultats précédents .. »