Modélisation des Système

Modélisation de systèmes linéaires 1. Systèmes linéaires 1.1 Définitions Système : amplificateur, moteur, mécanisme, combinaison de mécanique et d'électronique... tout système disposant d'une commande ou d'un signal d'entrée et restituant une grandeur en sortie. Système linéaire : Système dont les grandeurs caractéristiques sont liées par des équations différentielles linéaires à coefficients constants. [pic] figure 1 [pic] formule 1 exemple d'équation différentielle d'un système linéaire Les paramètres a1, a0, b2, b1 et b0 sont constants (ils ne varient pas avec le temps) et dépendent des éléments internes du système. L'ordre du système est défini par l'ordre de dérivé le plus haut. 1.2 Système linéaire du premier ordre Exercice 1 : quadripôle RC [pic] figure 2 1. Trouver la relation entre s(t), e(t), R et C. 2. Montrer que l'on peut mettre l'équation différentielle sous la forme canonique : Forme canonique [pic] formule 2 d'un système linéaire du premier? est la constante de temps ordre du système (s). 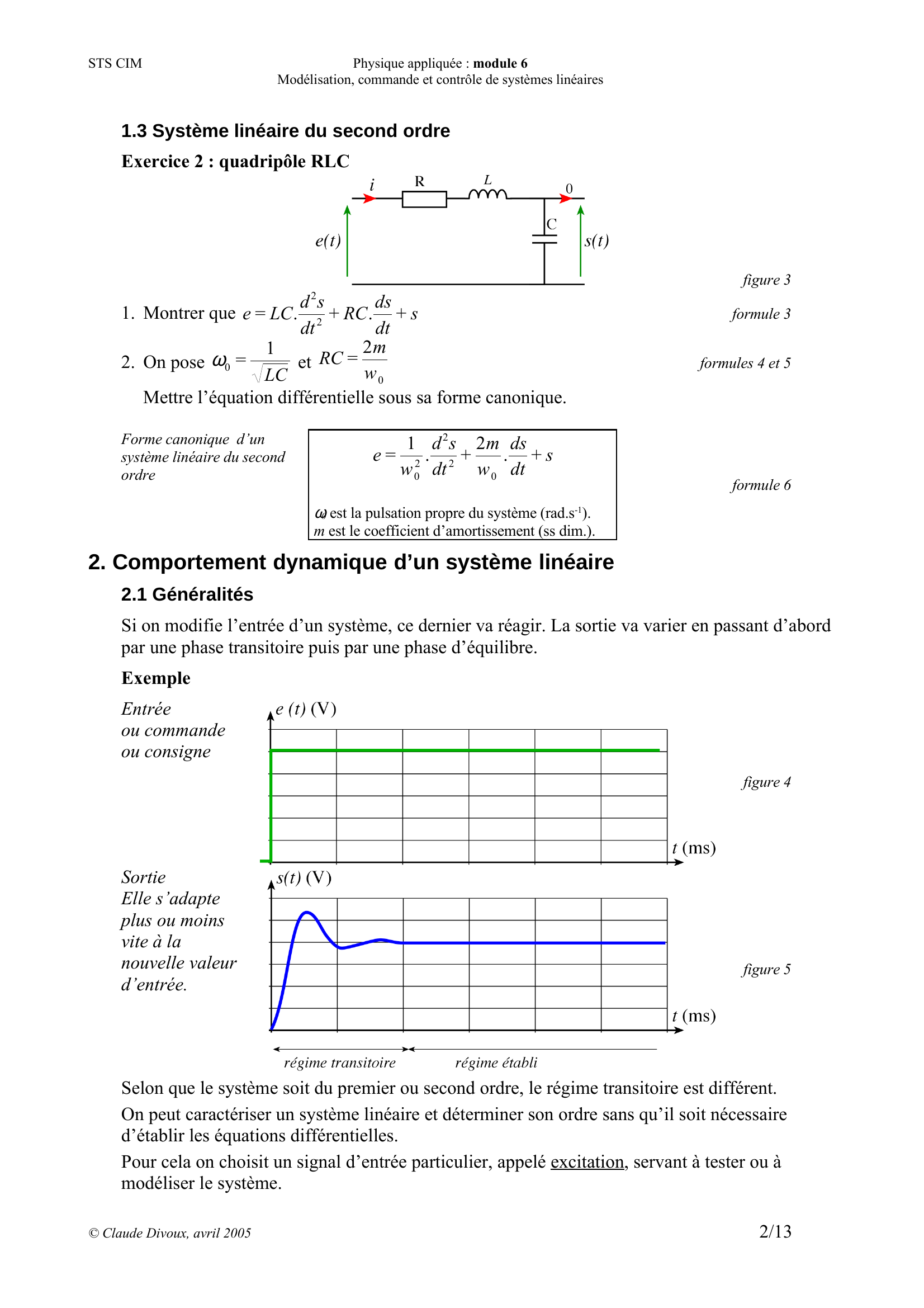1.3 Système linéaire du second ordre Exercice 2 : quadripôle RLC [pic] figure 3 1. Montrer que [pic] formule 3 2. On pose [pic] et [pic] formules 4 et 5 Mettre l'équation différentielle sous sa forme canonique. Forme canonique [pic] formule 6 d'un système linéaire du second?0 est la pulsation propre du ordre système (rad.s-1). m est le coefficient d'amortissement (ss dim.). 2. Comportement dynamique d'un système linéaire 2.1 Généralités Si on modifie l'entrée d'un système, ce dernier va réagir. La sortie va varier en passant d'abord par une phase transitoire puis par une phase d'équilibre. Exemple Entrée [pic] figure ou commande 4 ou consigne Sortie [pic] figure Elle s'adapte 5 plus ou moins vite à la nouvelle valeur d'entrée. Selon que le système soit du premier ou second ordre, le régime transitoire est différent. On peut caractériser un système linéaire et déterminer son ordre sans qu'il soit nécessaire d'établir les équations différentielles. Pour cela on choisit un signal d'entrée ...