MATHÉMATIQUE ET ACTION : Recherche de la stratégie optimale
Publié le 19/11/2011
Extrait du document
Le jeu d'entreprise que constitue une telle étude devient si complexe qu'il nécessite l'action de groupes, les uns spécialisés déterminant par exemple les découvertes que l'on peut attendre d'ici l'horizon économique fixé susceptible d'apporter des changements profonds, les autres interdi sciplinaires, confrontant les différentes contraintes. Pour cela il faut d'une part l'intervention d'ordinateurs puissants capables de fournir une analyse détaillée de toutes les tendances mesurables et de chiffrer les résultats des variations de tendance résultant de conflits et des équipes utilisant les méthodes les plus efficaces de la dynamique de groupe (certaines ont été spécialement créées pour cela : DELPHl par exemple) .
«
Fig.
où a, b, c ...
.
sont les prix unitaires, n•, n•, n• ..
les quantité s de produits à acheter et A la somme dont nous disposons.
Certes le problème peut ne pas être toujours aussi simple, les prix ne sont pas toujours proportionnels aux quan tités (réduction sur achat important), mais il est extrêmement rare que la variation soit conti nue, elle a lieu par paliers (a, le kg par achat de m oins de 5 kg, a• par 5 kg , a• par 50 kg, etc.)
ce qui nou s conduirait à examiner évrntuelle ment un certain nombre de relations du même type.
En général, notre problème comportera un certain nombre d'équations (se terminant par le signe =) ou d'inéquations (se terminant par < ou >) liant entre elles un certain nombre de variab l es qui n'ont de .signification qu'à con dition d'être posi tiv es ou nulles (dans notre exemple on peut acheter une certaine quantité d'un produit ou n'en pas acheter, on ne peut pas acheter une quantité négative).
Ces relations constituent les contraintes du phénomène.
Dans ce cadre on étud ie une f o nc tion linéaire de .
ces variable s, appelée gé n érale ment fonction éco n omique, que l'oq se proposera de rendre optim ale.
Prenons un exemple :
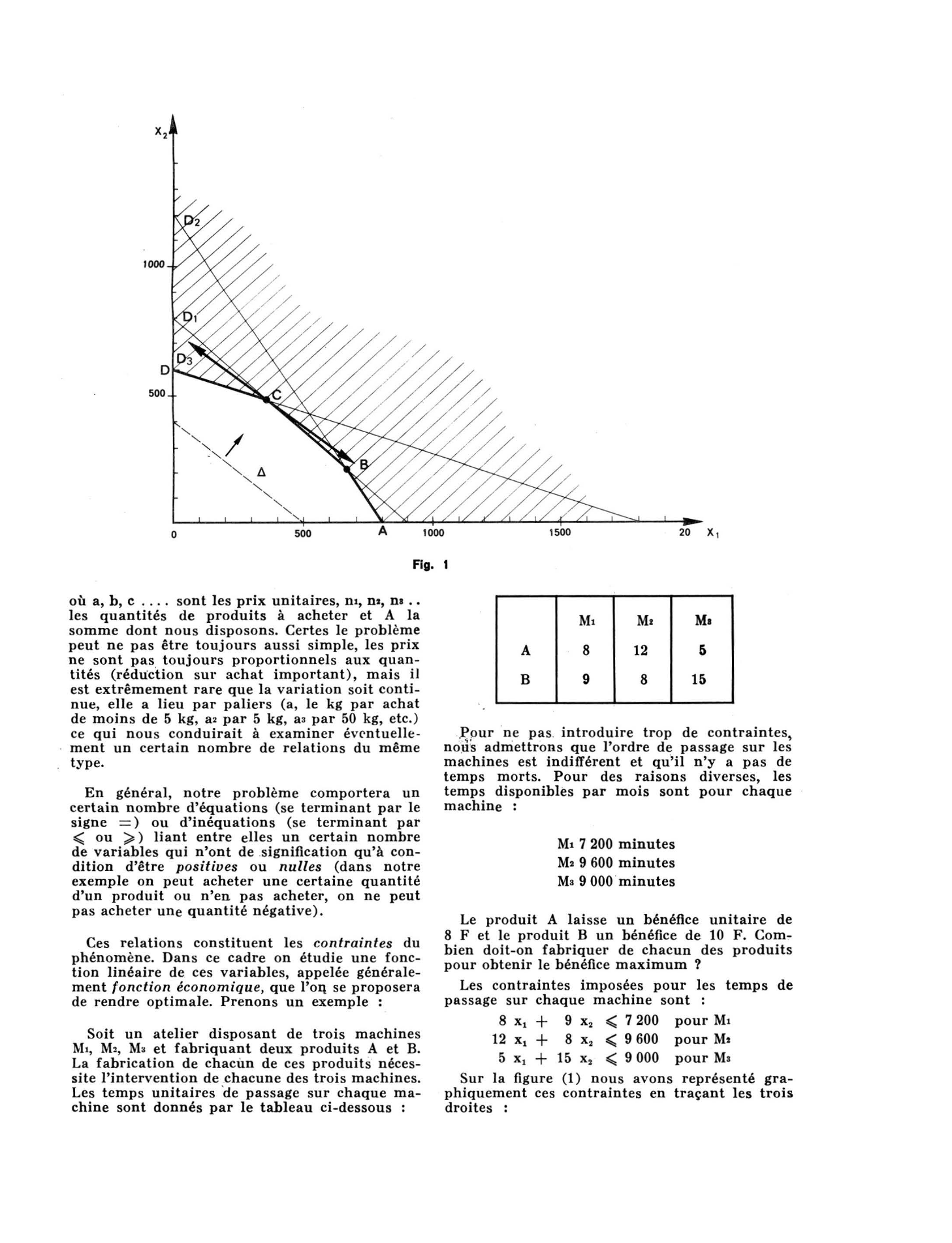
Soit un atelier disposant de trois machines M•, M•, M a et fabr iquant deux produits A et B.
La fabrication de chacùn de ces produits néces site l'intervention de chacune des trois machines.
Les temp s unitaires ·de passage sur chaque rna chine sont donnés par le tableau ci-dessous :
20 x,
Mt Mz Ma
A 8 12 6
B 9 8 16
.Pour ne pas .
introduire trop de contraintes, no)h admettrons que l'ordre de passage sur les machines est indifférent et qu'il n'y a pas de
t emps morts.
Pour des raisons diverses, les temps disponibles par mois sont pour chaque machine :
Mt 7 200 minutes
M• 9 600 minutes
M a 9 000 minutes
Le produit A laisse un bénéfi ce unitaire de
8 F et le produit B un bénéfice de 10 F .
Com bien doit-on fabriquer de chacun des produits pour obtenir le bénéfice maximum ?
Les
contra int es imposées pour les temps de passage sur chaque machine sont :
8 x, + 9 x, < 7 200 pour Mt
12 x, + 8 x, < 9 600 pour M•
5 x, + 15 x, < 9 000 pour Ma
Sur la figure (1) nous avons représenté gra phiquement ces contraintes en traç ant les trois droites :.
»
↓↓↓ APERÇU DU DOCUMENT ↓↓↓
Liens utiles
- Pratique de l’enquête coopérative : La recherche « avec » plutôt que « sur » les personnes in Handbook of Action Research (Peter Reason et Hillary Bradbury-Huan)
- l'action pratique peut-elle etre autre chose que la recherche du moindre mal ?
- L'action politique peut-elle être autre chose que la recherche du moindre mal ?
- L'action politique peut-elle être autre chose que la recherche du moindre mal ?
- MATHÉMATIQUE ET ACTION