LE COURANT ÉLECTRIQUE ALTERNATIF

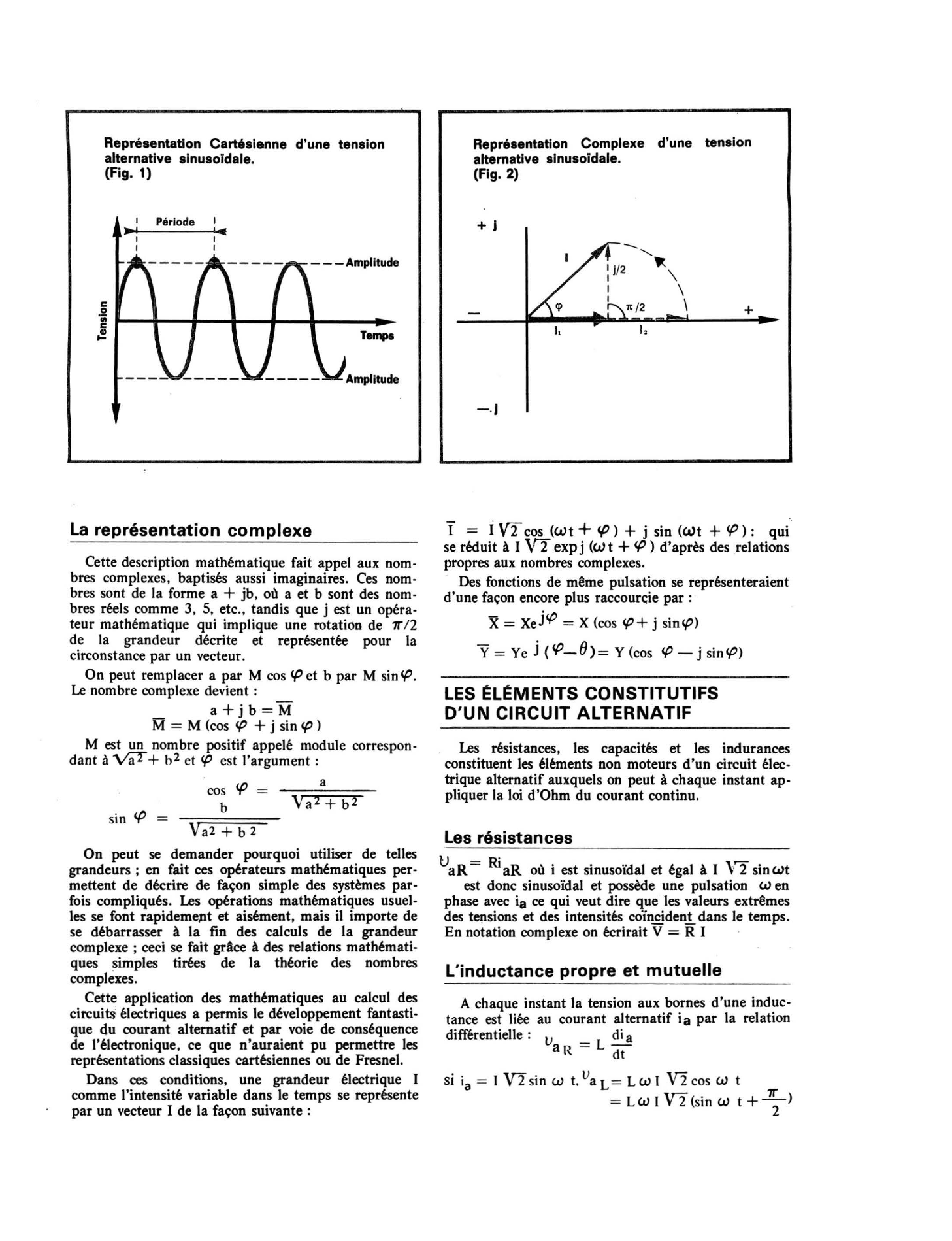
« Repréaentation Cartésienne d'une tension alternative sinusoïdale.

(Fig.

1) 1 Période t ,., 1 ...

1 1 1 1 ---Amplitude Tempa Amplitude La représentation complexe Cette description mathématique fait appel aux nom­ bres complexes, baptisés aussi imaginaires.

Ces nom­ bres sont de la forme a + jb, où a et b sont des nom­ bres réels comme 3, 5, etc., tandis que j est un opéra­ teur mathématique qui implique une rotation de 7r 12 de la grandeur décrite et représentée pour la circonstance par un vecteur.

On peut remplacer a par M cos 'Pet b par M sin 'P.

Le nombre complexe devient : a+jb=M M = M (cos ip + j sin '{) ) M est un nombre positif appelé module correspon­ dant à VaT+ h2 et ip est l'argument : sin 'P = cos 'P = b Va2 + b 2 a On peut se demander pourquoi utiliser de telles grandeurs ; en fait ces opérateurs mathématiques per­ mettent de décrire de façon simple des systèmes par­ fois compliqués.

Les opérations mathématiques usuel­ les se font rapideme,nt et aisément, mais il importe de se débarrasser à la fin des calculs de la grandeur complexe ; ceci se fait grâce à des relations mathémati­ ques simples tirées de la théorie des nombres complexes.

Cette application des mathématiques au calcul des circuitS électriques a permis le développement fantasti­ que du courant alternatif et par voie de conséquence de l'électronique, ce que n'auraient pu permettre les représentations classiques cartésiennes ou de Fresnel .

Dans ces conditions, une grandeur électrique 1 comme l'intensité variable dans le temps se représente par un vecteur 1 de la façon suivante : Représentation Complexe d'une tension alternative sinusoïdale.

(Fig.

2) + 1 + -.J Ï = i V2 cos (Wt + 'P) + j sin (Wt + if') : qui se réduit à 1 V2 exp j (wt + 'P) d'après des relations propres aux nombres complexes .

Des fonctions de même pulsation se représenteraient d'une façon encore plus raccourcie par : X= Xejlf' =X (cos IP+ j sinip) Y= Ye j ('P-8)= Y (cos 'P- j sin if') LES t:Lt:MENTS CONSTITUTIFS D'UN CIRCUIT ALTERNATIF Les résistances, les capacités et les indurances constituent les éléments non moteurs d'un circuit élec­ trique alternatif auxquels on peut à chaque instant ap­ pliquer la loi d'Ohm du courant continu.

Les résistances UaR = Ri aR où i est sinusoïdal et égal à 1 VI sinwt est donc sinusoïdal et possède une pulsation w en phase avec ia ce qui veut dire que les valeurs extrêmes des tensions et des intensités coïn~den.!_ dans le temps.

En notation complexe on écrirait V = R 1 L'inductance propre et mutuelle A chaque instant la tension aux bornes d'une induc­ tance est liée au courant alternatif i a par la relation différentielle : u di a aR= L dt si i8 = 1 V2 sin w t.

ua L = Lw 1 Vï cos w t = LW 1 V2 (sin W t + ~ ). »