La chute des « graves » L'oscillation des corps pesants

« grès de la pensée et du rôle de l'erreur dans la recherche scientifique.

La proportion simple que Galilée croit devoir placer natu­ rellement à la base de sa construction, en 1604, est en effet fausse et aurait dû le conduire à une loi de la chute bien diffé­ rente de celle qu'il s'agissait pour lui de démontrer.

S'il parvient cependant à la retrouver, c'est grâce à des erreurs succes­ sives de raisonnement qui se compensent.

Cela, on l'a maintes fois mis en évidence sans remarquer le danger qu'il y a à juger du passé en fonction du présent, c'est-à­ dire d'une manière plus précise, en fonction du matériel mental que nous possédons présentement.

La leçon des erreurs du passé, qu'il importe de saisir au suprême degré, n'est possible que dans un effort d'abstraction par rapport à ce matériel mental présent.

Or lorsqu'on parle de vitesse, le moderne voit immédiatement le rapport instantané de la variation d'espace à la variation du temps, il n'a pas de peine à concevoir la vitesse comme une grandeur mathématique, une fonction de même type que toute autre.

C'était précisément ce qui gênait Aristote, c'était encore ce qui restait obscur pour un Galilée.

Qu'est-ce que la vitesse ? La question restera sans réponse nette jusqu'à la fin du xvll 8 siècle.

Pour comprendre quelque chose a la véri­ table comédie des erreurs que constituent les spéculations sur la chute des graves, c'est à cette difficulté centrale qu'ilconvient de se référer.

Avant Galilée.

Lorsque Galilée entreprend en 1604 son essai de démonstration de la chute des graves, la question est loin d'être entière, il hérite d'un double courant dont il importe de dire quelques mots.

Un courant « cinématique »tout d'abord, particulièrement manifeste chez Albert de Saxe, William Heytesbury (Oxford), et Nicole Oresme (deuxième moitié du xive siècle).

Ce dernier applique au mouvement une représentation graphique conçue pour traduire d'une manière générale toute • qualité • variable • au sein d'un sujet ».

Sous une forme confuse cette représen­ tation graphique n'est autre que celle qui nous est familière par l'usage de deux axes de coordonnées.

L'abscisse représente le • sujet » sous l'aspect où on le considère, l'ordonnée la« qualité • correspondante.

La vitesse dans un corps est une qualité dou­ blement variable en droit, variable d'un point à un autre et variable dans le tem~s.

L'image de la vitesse par l'intermédiaire d'un graphique est donc possible de deux manières, suivant que l'on porte en abscisse l'extension dans le temps ou l'extension dans l'espace.

Dans les deux cas, pour un mobile ponctuel, l'image du mouvement uniforme n'est pas, comme le lecteur mo­ derne s'y attendrait, une droite horizon­ tale, mais c'est un rectangle.

Car Oresme voit dans un seul regard l'ensemble de toutes les ordonnées égales, représentatives de la « qualité » uniforme qui est par défi­ nition la même partout et toujours, et l'ensemble de ces ordonnées constitue une surface, mesure de la qualité totale et donc aussi de la qualité donnée.

C'est par ce tru­ chement que la vitesse du mouvement unüorme apparaît avoir une mesure totale proportionnelle à l'espace parcouru, le rectangle de hauteur constante ayant une surface proportionnelle à sa longueur.

Dans le cas de qualités non uniformes, ou, comme le dit Oresme, difformes, le gra­ phique fait apparaître une aire limitée par une courbe.

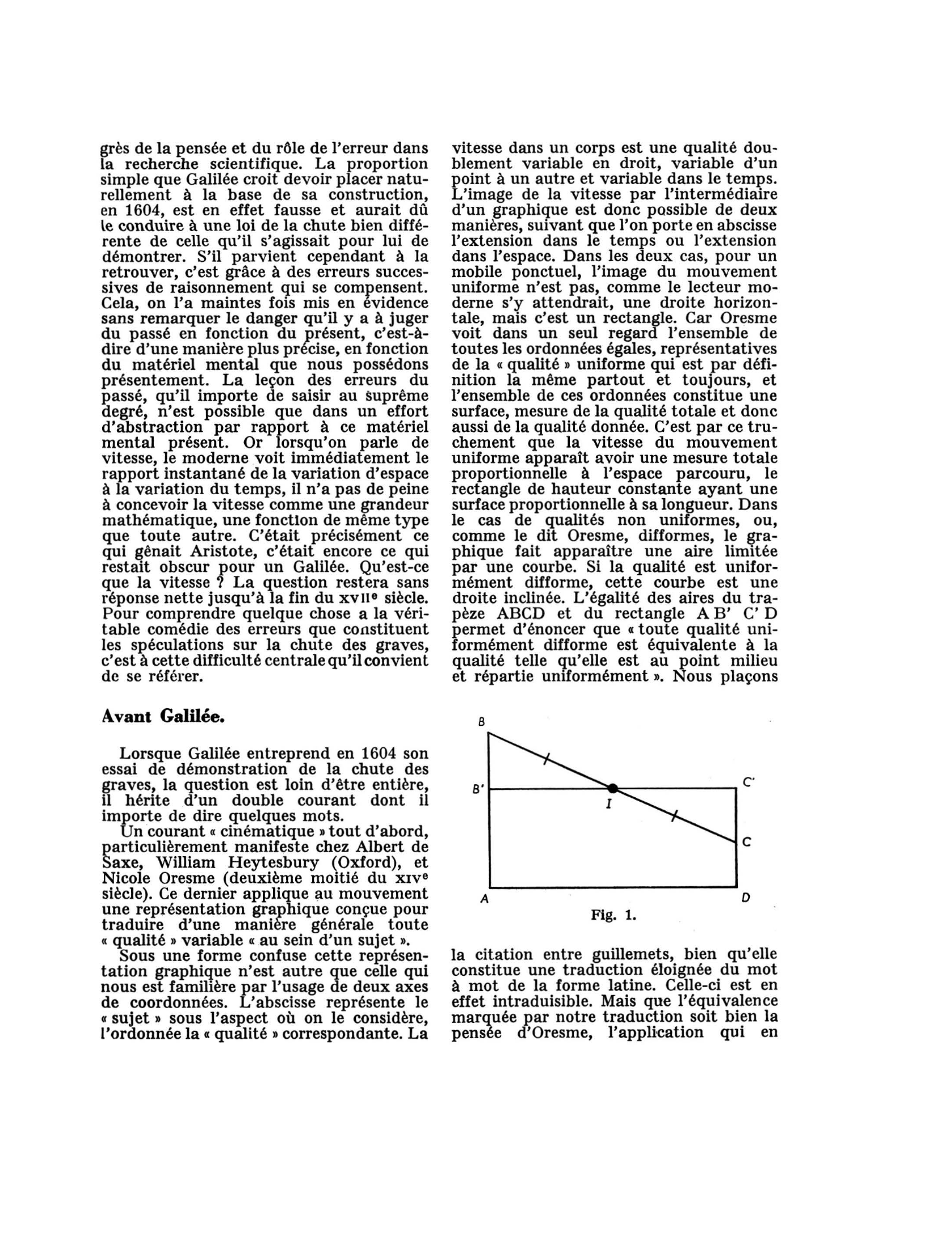
Si la qualité est unifor­ mément düforme, cette courbe est une droite inclinée.

L'égalité des aires du tra­ pèze ABCD et du rectangle AB' C' D permet d'énoncer que «toute qualité uni­ formément difforme est équivalente à la qualité telle qu'elle est au point milieu et répartie umformément ».

Nous plaçons B A Fig.

1.

la citation entre guillemets, bien qu'elle constitue une traduction éloignée du mot à mot de la forme latine.

Celle-ci est en effet intraduisible.

Mais que l'équivalence marquée par notre traduction soit bien la pensée d'Oresme, l'application qui en. »