Bac S - France métropolitaine – Septembre 2004 - Mathématique

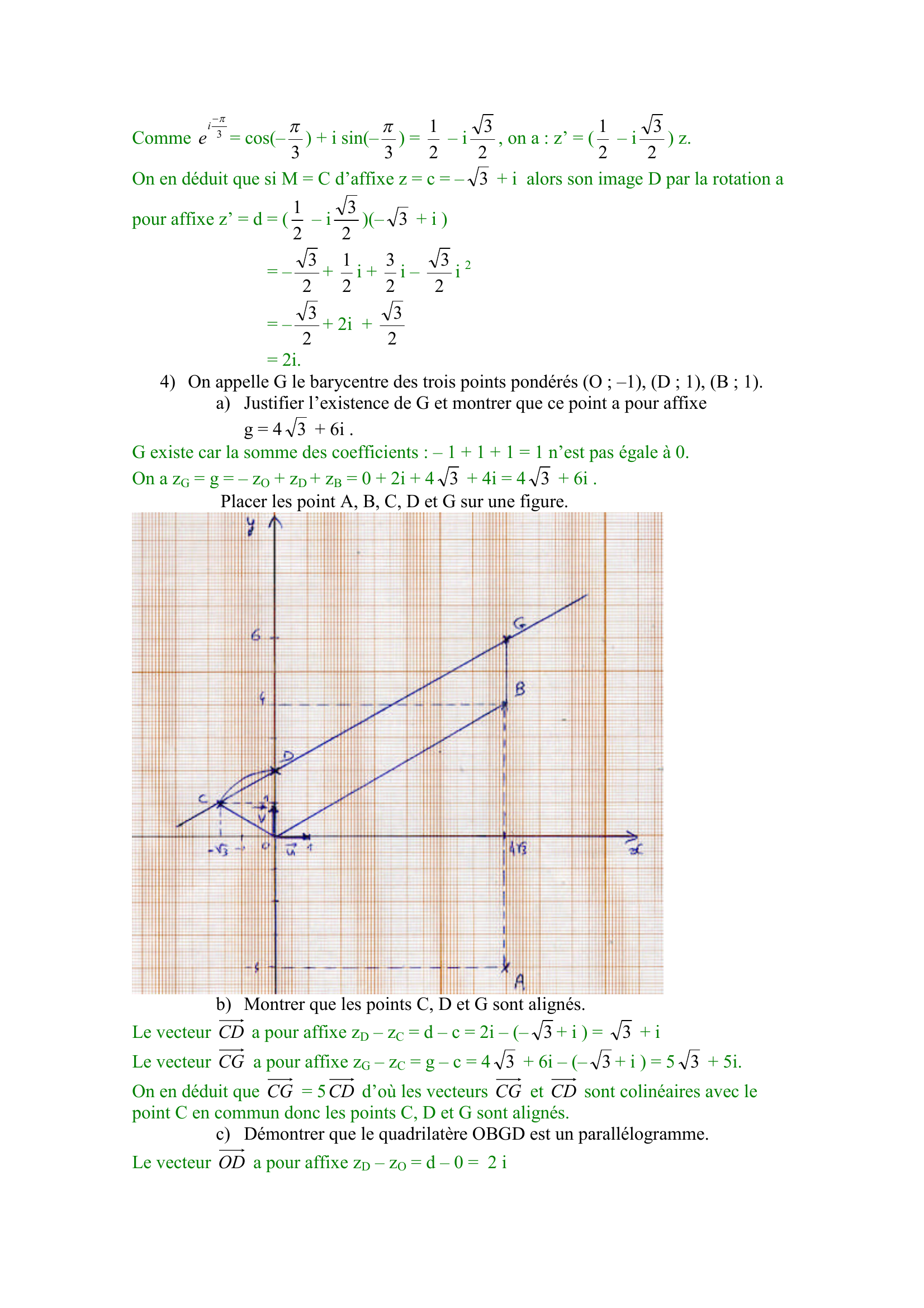
« Comme 3 ie = cos(– 3  ) + i sin(– 3  ) = 2 1 – i 2 3, on a : z’ = ( 2 1 – i 2 3) z. On en déduit que si M = C d’affixe z = c = – 3 + i alors son image D par la rotation a pour affixe z’ = d = ( 2 1 – i 2 3)(– 3 + i ) = – 2 3+ 2 1i + 2 3i – 2 3i2 = – 2 3+ 2i + 2 3 = 2i. 4) On appelle G le barycentre des trois points pondérés (O ; –1), (D ; 1), (B ; 1). a) Justifier l’existence de G et montrer que ce point a pour affixe g = 4 3 + 6i . G existe car la somme des coefficients : – 1 + 1 + 1 = 1 n’est pas égale à 0. On a z G= g = – z O+ z D+ z B= 0 + 2i + 4 3 + 4i = 4 3 + 6i . Placer les point A, B, C, D et G sur une figure. b) Montrer que les points C, D et G sont alignés. Le vecteur CD a pour affixe z D– z C= d – c = 2i – (– 3+ i ) = 3 + i Le vecteur CG a pour affixe z G– z C= g – c = 4 3 + 6i – (– 3+ i ) = 5 3 + 5i. On en déduit que CG = 5 CD d’où les vecteurs CG et CD sont colinéaires avec le point C en commun donc les points C, D et G sont alignés. c) Démontrer que le quadrilatère OBGD est un parallélogramme. Le vecteur OD a pour affixe z D– z O= d – 0 = 2 i. »