T2C11 : Mouvement et deuxième loi de Newton

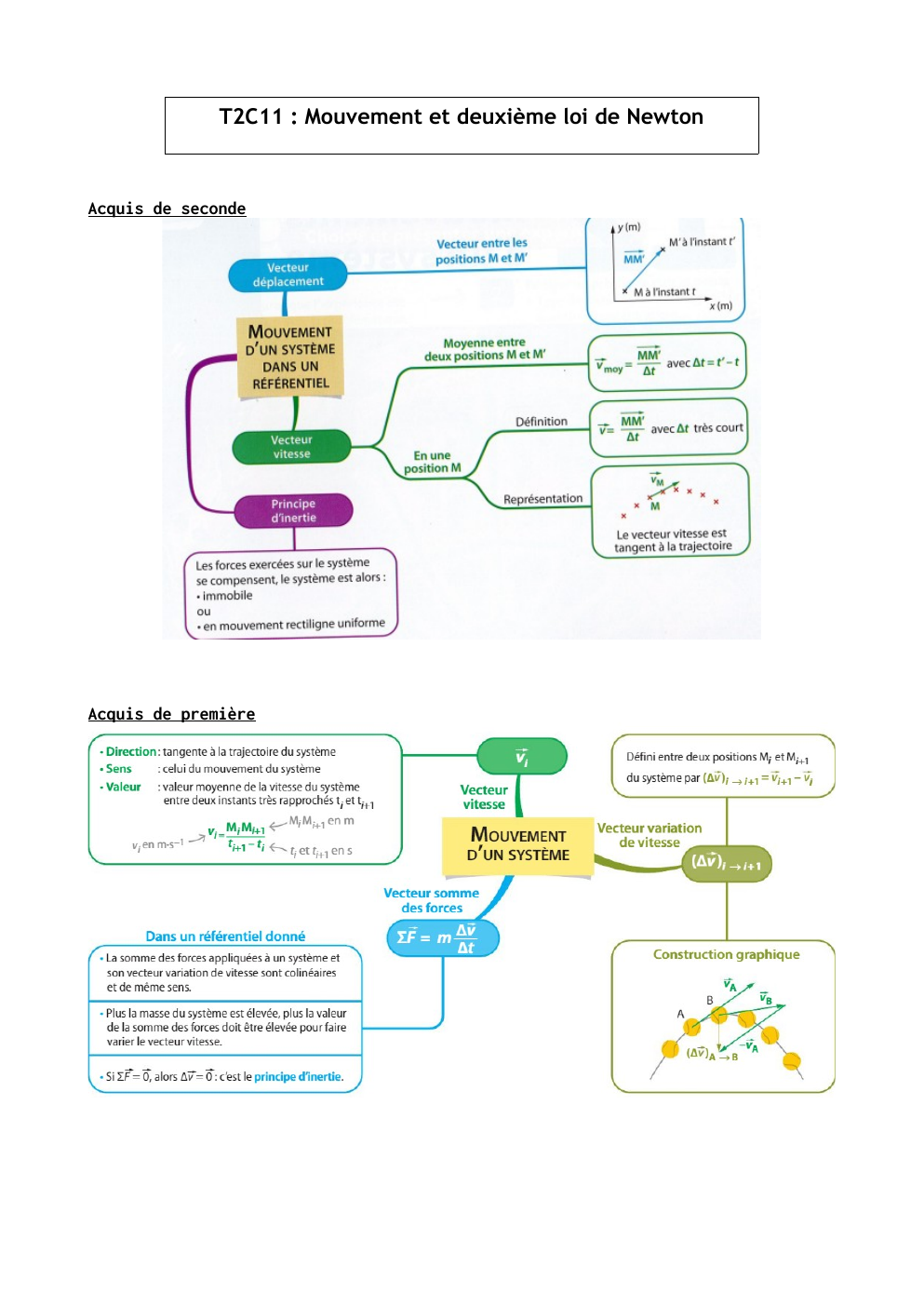
« T2C11 : Mouvement et deuxième loi de Newton Acquis de seconde Acquis de première Tracé du vecteur variation de vitesse 3-4 Le vecteur variation de vitesse est directement proportionnel à la somme des forces extérieures appliquées au système Système d’étude : on se limitera à l’étude d’un point particulier du système appelé (centre d’inertie) centre de masse qui a le mouvement le plus simple. Référentiel : Le mouvement d’un corps doit être décrit par rapport à un solide de référence. On le choisit arbitrairement mais on préfère choisir un type de référentiel appelé galiléens : Un référentiel est galiléen si dans celui-ci le principe d’inertie est vérifié. Dans nos études, le plus souvent, on utilise des référentiels terrestres, ils sont liés à n’importe quel objet fixe par rapport au sol terrestre et ils sont considérés galiléen . La trajectoire est l’ensemble des positions successives occupées par le système au cours de son mouvement, elle est visible avec des enregistrements ou des chronophotographies Vecteur position (unité de la valeur du vecteur position le mètre : m) On appelle vecteur-position le vecteur qui relie l’origine du repère au point 𝑀 étudié.  Pour décrire un mouvement il faut avoir une notion de temps.

On introduit la date t qui correspond à l’intervalle de temps entre l’instant de date t et un instant pris comme origine t = 0  Il faut un repère d’espace orthonormé dans lequel un point M sera repéré par 3 coordonnées (x, y, z)  Ces trois coordonnées du vecteur position sont fonctions du temps si le point est mobile. Vecteur vitesse (unité de la valeur : m.s-1 )  Appliqué en G (centre de gravité)  De direction : la tangente à la trajectoire  De sens : celui du mouvement.  Expression : dérivée du vecteur position d⃗ OM ⃗ V= dt Vecteur accélération (unité de la valeur m.s-2 )  Appliqué en G (centre de gravité) V  De direction et de sens : celui de Δ ⃗  Expression : dérivée du vecteur vitesse d⃗ V ⃗a = dt Pour tracer le vecteur vitesse, il existe deux méthodes graphiques : → la méthode approchée (celle utilisée dans votre livre et donc en classe), moins précise pour les mouvements circulaires ou curvilignes → la méthode centrée (qui peut être employée dans un exercice de bac) méthode approchée : méthode centrée : même origine, même direction et même sens que pour l’autre méthode mais avec une valeur qui se calcule avec les deux points voisins du point considéré : M i +1−M i−1 Vi = t i +1−t i−1 Le vecteur accélération est tracé graphiquement à partir du vecteur variation de vitesse : a4 : Exemple pour tracer le vecteur accélération au point 4 noté ⃗ V 4 pour la V 3 et ⃗ il faut tracer les vecteur ⃗ méthode approchée ou ⃗ V5 V 3 et ⃗ pour la méthode centrée Astuce graphique A partir du graphe x(t) par exemple,.... »