Réponse d'une bobine à un échelon de tension

3. Détermination de la valeur numérique de z à partir de l'exploitation

théorique de la courbe d'établissment du courant

Le circuit étudié est celui proposé en 1.

En utilisant la relation d'additivité des tensions dans un circuiit série, on

obtient l'équation différentielle régissant l'établissment du courant dans le

d i

circuit : E = Ri + L _d—_t.

a)      Vérifier que —^L est homogène à un temps. R

b)     Quelle est la valeur de l'intensité à la date t = 0 s ? Comment s'écrit alors l'équation différentielle donnée précédemment ?

c)      Déterminer, à la date t = 0 s, l'expression de ⁱ. En déduire l'équation d t

de la tangente à la courbe d'établissement du courant à la date t = 0 s, et

montrer que cette droite passe par i = I en t = T.

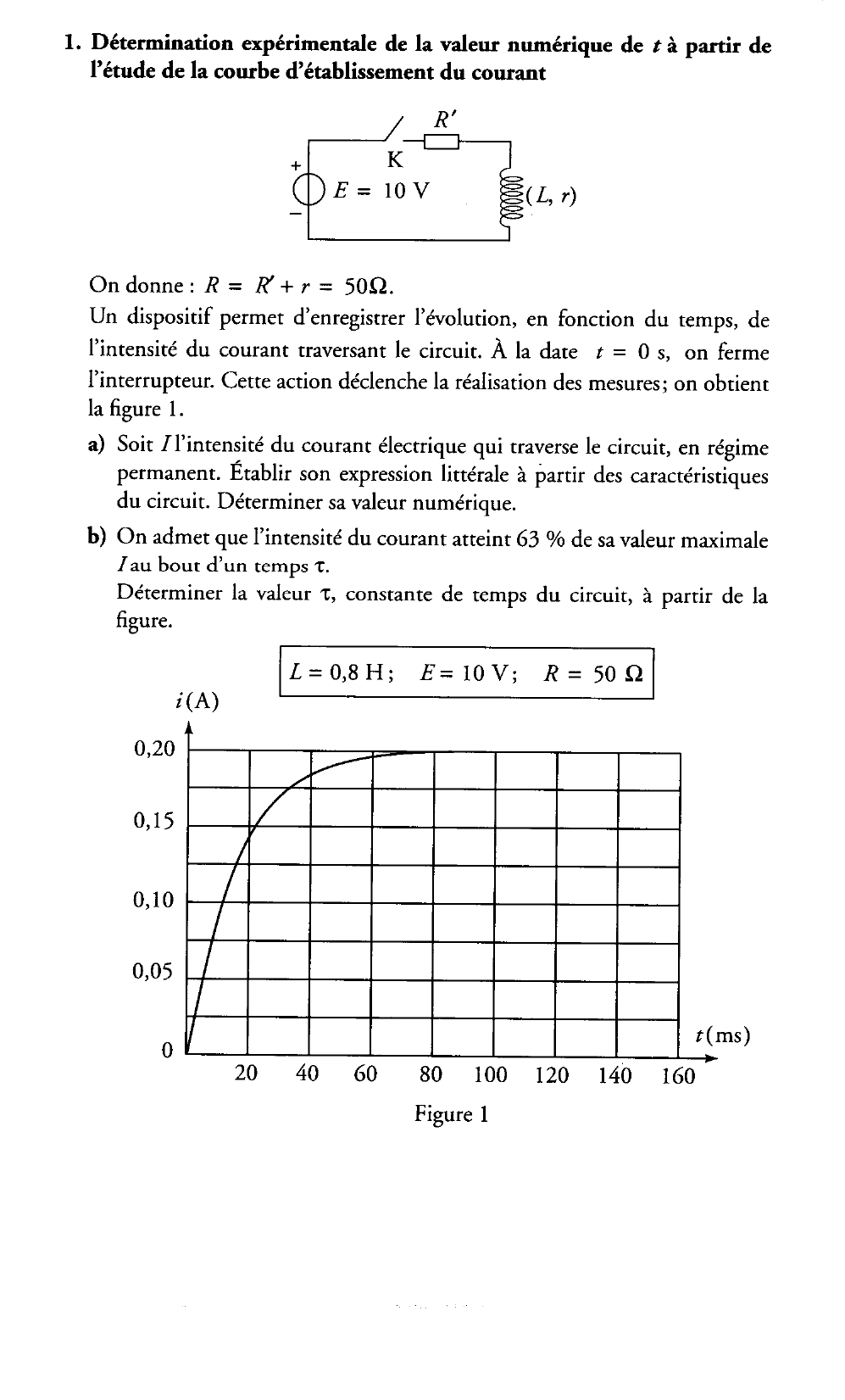
Déduire graphiquement, de la figure 3, la valeur numérique de T.

On se propose d'étudier l'établissement du courant au travers d'une bobine inductive et résistive lorsque celle-ci est soumise à un échelon de tension. Pour obtenir une indication sur la durée nécessaire à l'établissement d'un régime per­manent, on utilise la grandeur notée 'c, appelée constante de temps du circuit et

définie par       = R.