EXERCICES TYPES : DIPÔLE R, C - EXPLOITATION DES COURBES U(t) et l(t)

« 336 .2 .

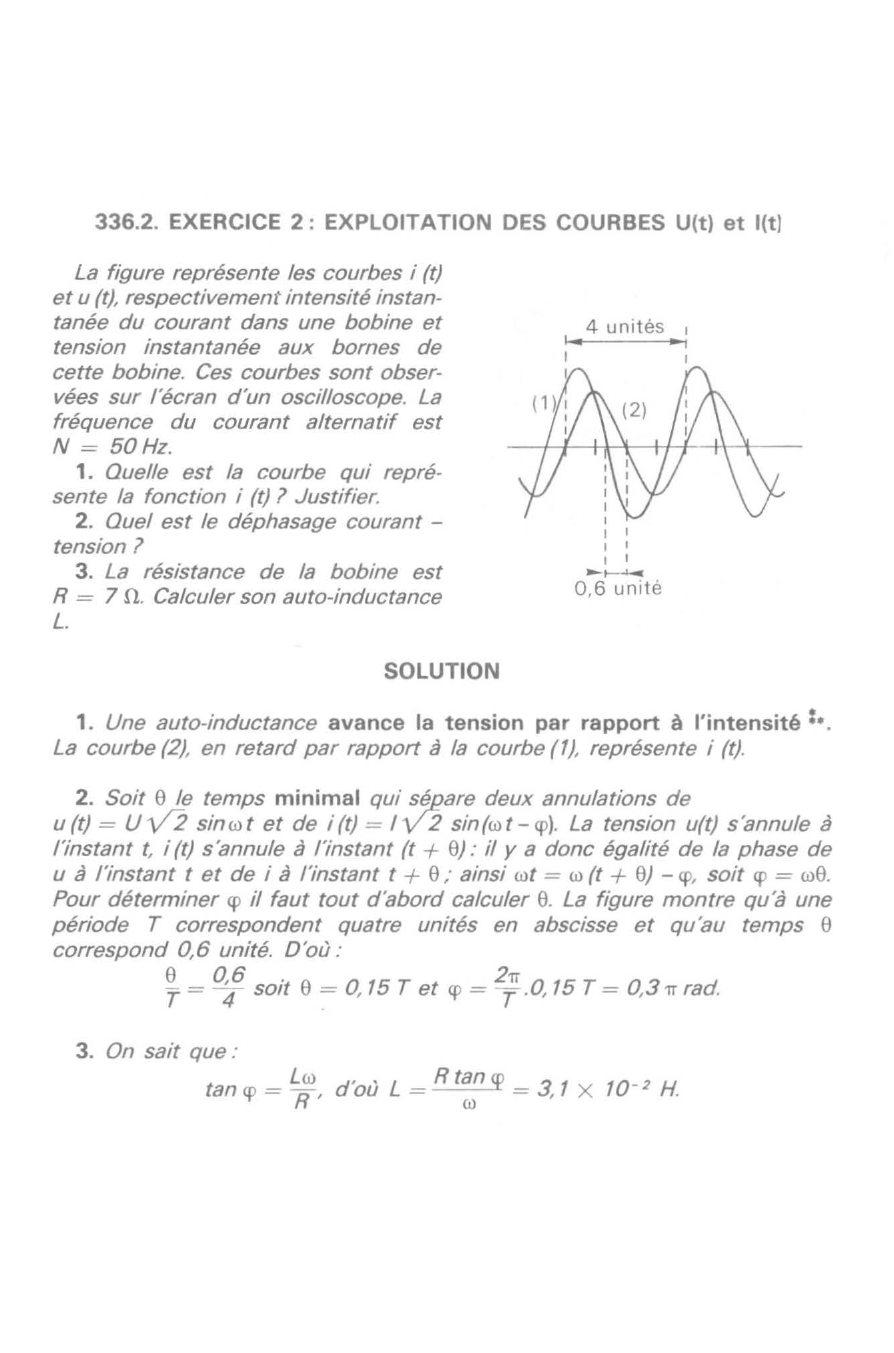
EXERCICE 2 : EXPLOITATION DES COURBES U(t) et l(t) La figure représente les courbes i (t) et u (t) , respectivement intensité instan­ tanée du courant dans une bobine et tension instantanée aux bornes de cette bobine .

Ces courbes sont obser­ vées sur l'écran d'un oscilloscope .

La fréquence du courant alternatif est N = 50Hz .

1.

Quelle est la courbe qui repré­ sente la fonction i (t) ? Justifier .

2.

Quel est le déphasage courant - tension? 3.

La résistance de la bobine est R = 7 n .

Calculer son auto-inductance L.

SOLUTION ' 1 1 1 _,_...._..

0,6 un it é 1.

Une auto-inductance avance la tension par rapport à l'intensité : •.

La courbe (2} , en retard par rapport à la courbe (1), représente i (t).

2.

Soit e le temps minimal qui s~are deux annulations de u(t) = UV2 sinwt et de i(t) =IV 2 sin( wt- cp).

La tension u(t) s'annule à lïnstant t.

i (t) s'annule à l'instant (t + e): il y a donc égalité de la phase de u à lïnstant t et de i à lïnstant t + e; ainsi wt = w (t + e) -cp, soit cp = we.

Pour déterminer cp il faut tout d 'abord calculer e.

La figure montre qu'à une période T correspondent quatre unités en abscisse et qu'au temps e correspond 0,6 unité .

D ' où : ~ = 046 soit e = 0, 15 T et cp = 2;.

0, 15 T = 0,3 1r rad.

3.

On sait que : tan cp= '-; .

d 'où L = R t~n P = 3,1 x 10 - 2 H.. »