TD Cours Math-SES Corrigé et compléments Courbe de Lorenz
Publié le 17/04/2014

Extrait du document

Objectif du TD : étude des inégalités de répartition des revenus des ménages et comparaison avec le patrimoine , mise en évidence à l'aide de graphiques et d'indicateurs ( courbe de Lore nz et coefficient de Gini ) Les données, tableaux et graphiques proviennent de l'étude de l'INSEE : « les revenus et patrimoines des ménages, édition 2006 » d'après l'enquête 2003-2004. Partie A : revenus disponibles des ménages : construction d'une courbe de Lorenz I- caractéristiques de dispersion d'une série statistique : médianes , quartiles , déciles . Les données collectées lors d'une enquête sont regroupées en vue d'une étude statistique pour être analysées et commentées. Un graphique de base : le regroupement par classe Tableau des effectifs et des fréquences xi [;[ [ ;[ .... [ ;[ effectifs : ni fréquences : fi remarque : sur ce graphique de l'INSEE, les effectifs sont ramenés en pourcentage de l'effectif total ( c'est-à-dire du nombre total de ménages), en ordonnée sont donc représentées les fréquences de la série statistique. (Les données sont regroupées par ordre croissant du revenu.) l'avantage de ce type de graphique est de voir la répartition des revenus par classe d'amplitude 100 EUR mais ne permet pas une interprétation en terme de dispersion (1) Pour mettre en évidence les caractéristiques de dispersion de la série statistique, on détermine la médiane, les quartiles et les déciles. Pour cela, on établit le tableau des fréquences cumulées croissantes ou des effectifs cumulés croissants ( obtenu directement à l'aide de logiciels lorsqu'il y a de nombreuses données ) xi [;[ [ ;[ .... [ ( x12 pour le revenu annuel ) ;[ fréquence : fi fréquences cumulées 100% (2) A l'aide de la lecture du graphique ci-contre, compléter le tableau suivant : Premier décile D1 Premier quartile Q1 médiane Troisième quartile Q3 Dernier décile D9 11500 16 000 25000 36000 50000 2 Attention : D1,Q1, Me, Q3 et D9 sont des valeurs du caractère de la série statistique. (3) Construire le diagramme en boîte appelé aussi « boîte à moustache » associé à cette série statistique 1 En math, on demandera souvent la valeur de l'écart interquartile : Q3-Q1 = 36000-16000 = 20000 EUR Interprétation : l'écart des revenus annuels disponibles des ménages entre les 25 % les plus riches et les 25% les plus pauvres est supérieur à 20 000 EUR. 50000 En SES , on demandera plutôt les rapports interdéciles : exemple D9 ? ? 4,3 D1 11500 Interprétation : le revenu des 10% les plus riches est au moins 4,3 fois supérieur au revenu des 10 % les plus pauvres. Vision des quartiles et l'écart interquartile sur l' histogramme des fréquences ( graphique n°1 ) .On a hachuré les 25% des effectifs des valeurs en dessous de Q1 et les 25% des effectifs des valeurs au dessus de Q3 ( les aires des parties hachurées sont donc éga les), 50 % des effectifs sont donc entre Q1 et Q3. (4 ) Remarque : en SES, On emploie aussi le terme de décile pour désigner les ensembles (au nombre de 10) des données situées entre deux déciles ( déciles pointés ) par exemple pour D6 : ensemble des valeurs de la série obtenues entre 50 % et 60 % des effectifs ) . On obtiendrait pour D6 : ] 25 000 ; 29 000 ]. Les 10 % des ménages ayant un revenu supérieur à celui des 50 % les moins riches et inférieur à celui des 40 % les plus riches, ont un revenu compris entre 25 000 EUR et 29 000 EUR . (5) R Les aires vertes entre chaque décile sont égales. 2 Rappel : ne pas confondre moyenne et médiane ! Que signifierait le constat d'un revenu moyen supérieur au revenu médian ? Rappel : la moyenne est aussi égale à la moyenne des moyennes des sous groupes affectés de leur proportion . Ainsi, la moyenne des salaires de tous les ménages est égale au milieu (6) de la moyenne des revenus des 50 % les plus riches et de la moyenne des 50% les moins riches. L' écart entre le revenu médian et le revenu moyen des 50 % des ménage s les plus riches est bien plus important que l'écart entre le revenu médian et le revenu moyen des 50 % les moins riches. Interprétation : la proportion des ménages ayant un revenu inférieur au salaire moyen est supérieure à la proportion des ménages a yant un salaire supérieur au revenu moyen . On en conclut que ceux qui ont un salaire supérieur au revenu moyen perçoivent un revenu beaucoup plus élevé que les autres. La moyenne est sensible aux valeurs extrêmes alors que la médiane ne l'est pas , d'où le choix de l'indicateur de la médiane plutôt que celui de la moyenne dans l' étude qui suit.( mais l'une et l'autre se complètent ! d'où le tableau ci-dessus fourni par l'INSEE ) 3 compléments sur la calcul de la moyenne. Pour calculer la moyenne des revenus de l'ensemble des ménages à l'aide d'un tableau par regroupement par classe, on multipli e les effectifs ( ou les fréquences) par le centre de la classe, mais ce calcul ne permet que d'en trouver une valeur approchée : on ne sait pas comment sont répartis les revenus dans chaque classe . Pour la valeur exacte, on fait le calcul sur toutes les données ( fai t par le logiciel) ou on peut se servir d'un autre tableau fourni par l'INSEE : Ainsi on pourra calculer la moyenne des revenus sachant que les ménages dans chaque tranche gagnent en moyenne le revenu moyen de la tranche ( on calcule la moyenne à partir des moyennes des sous groupes ) : 0,1?8790 + 0,1?13010+ 0,1?15940+ 0,1?19250+ 0,1?22780+ 0,1?26570+ 0,1?30840+ 0,1?36080+ 0,1?43930+ 0,1?72170 = 28936 EUR On retrouve bien s&ucir...

«
2
En math, on demandera souvent la valeur de l’écart interquartile : Q3 -Q1 = 36000 -16000 = 20000 €
Interprétation : l’écart des revenus annuels disponibles des ménages entre les 25 % les plus riches et les 25% les plus pauvres est
supérieur à 20 000 €.
En SES , on demandera plutôt les rapports interdéciles : exemple
Interprétation : le revenu des 10% les plus riches est au moins 4,3 fois supérieur au revenu des 10 % les plus pauvres.
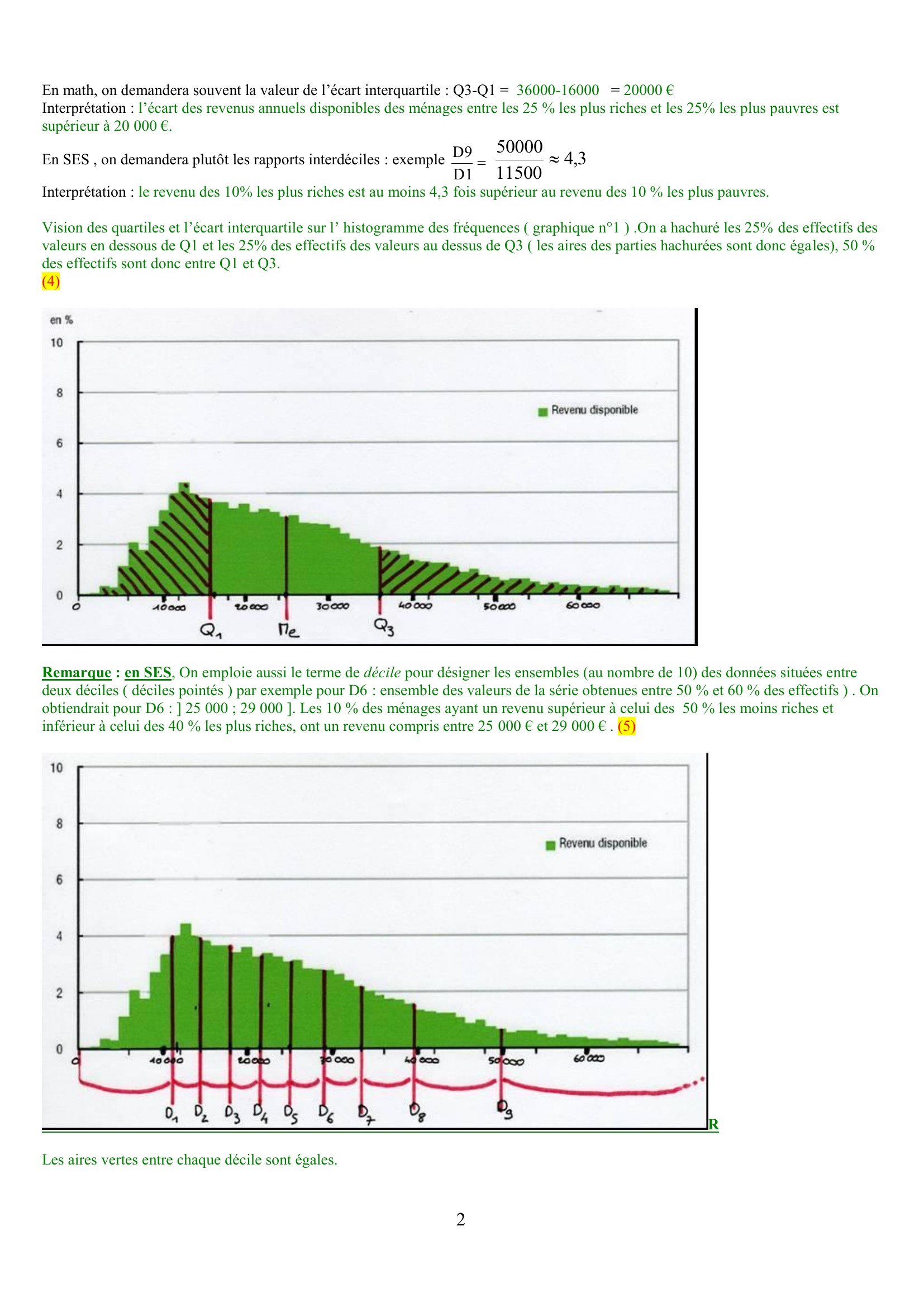
Vision des quartiles et l’écart interquartile sur l’ histogramme des fréquences ( graphique n°1 ) .On a hachuré les 25% des effectifs des
valeurs en dessous de Q1 et les 25% des effectifs des valeurs au dessus de Q3 ( les aires des parties hachurées sont donc éga les), 50 %
des effectifs sont donc entre Q1 et Q3.
(4)
Remarque : en SES , On emploie aussi le terme de décile po ur désigner les ensembles (au nombre de 10) des données situées entre
deux déciles ( déciles pointés ) par exemple pour D6 : ensemble des valeurs de la série obtenues entre 50 % et 60 % des effectifs ) .
On
obtiendrait pour D6 : ] 25 000 ; 29 000 ].
Les 10 % des ménages ayant un revenu supérieur à celui des 50 % les moins riches et
inférieur à celui des 40 % les plus riches, ont un revenu compris entre 25 000 € et 29 000 € . (5)
R
Les aires vertes entre chaque décile sont égales.
D1
D9 3,4 11500
50000 .
»
↓↓↓ APERÇU DU DOCUMENT ↓↓↓
Liens utiles
- cours fonction égalité inégalité math
- Acides Carboxyliques et dérivés d'acides Compléments du cours de l'UE1 qui est un pré-requis 1 Acides
- Tutorat 2004-2005 Biologie - Corrigé du sujet n°2 Questions de cours : (8 points) 1) Les différents types de jonctions intercellulaires: ( 2 points) Citer les différents types de jonctions intercellulaires pouvant exister entre deux cellules, précisez leurs noms et leurs structures.
- La conscience de soi rend-elle libre ? (Corrigé) Problématisation
- Cours d'histoire-géographie 2nd