Repère coord corrigé
Publié le 01/12/2014

Extrait du document
«
2de C02 _R EPÈRES -C OORDONNÉES D ’ UN P T _ DS03_ C ORRIGÉ
▪ EF² = ( x
E – x
F )² + (y
E – y
F )² = ( 12
– (1+
3
2 ))² + (
3
2 – 1 2
)²
EF² = (– 1
2
–
3
2 )² + (
3
2 – 1 2
)² Þ EF = 2
▪ DF² = ( x
D – x
F )² + (y
D – y
F )² = (0 – (1+ 3
2 ))² + (1– 1
2
)²
DF² = 2+
3 Þ DF =
2 + 3 = 6 - 2
2
▪ DE + EF =
6 + 2
2 + 2 = 6 2
2 -
= DF.
Conclusion : Les points D, E et F sont alignés.
Ex.
1 (12 pts)
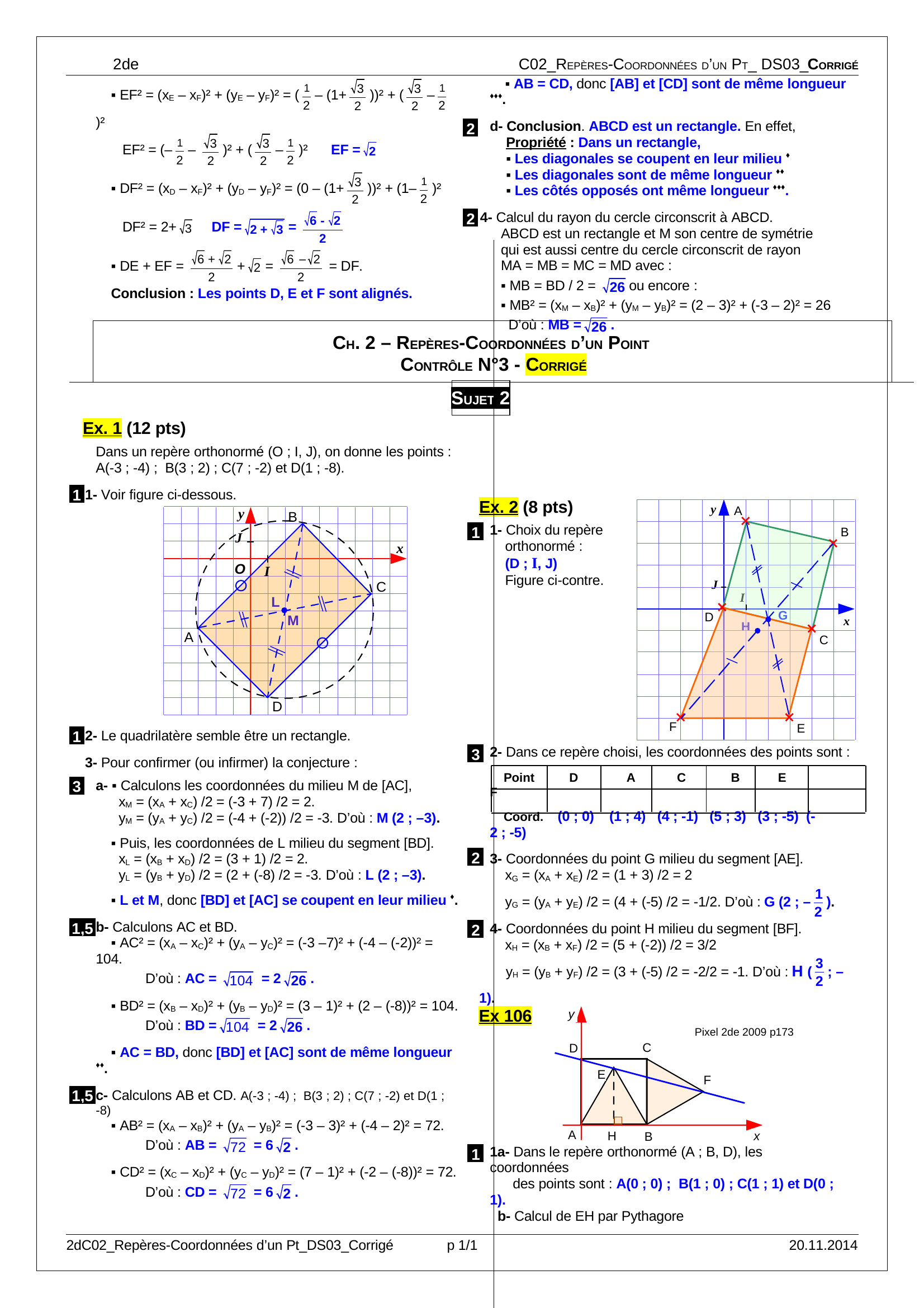
Dans un repère orthonormé (O ; I, J), on donne les points :
A(-3 ; -4) ; B(3 ; 2) ; C(7 ; -2) et D(1 ; -8).
1- Voir figure ci-dessous.
2- Le quadrilatère semble être un rectangle.
3- Pour confirmer (ou infirmer) la conjecture :
a- ▪ Calculons les coordonnées du milieu M de [AC],
x
M = (x
A + x
C ) /2 = (-3 + 7) /2 = 2.
y
M = (y
A + y
C ) /2 = (-4 + (-2)) /2 = -3.
D’où : M (2 ; –3) .
▪ Puis, les coordonnées de L milieu du segment [BD].
x
L = (x
B + x
D ) /2 = (3 + 1) /2 = 2.
y
L = (y
B + y
D ) /2 = (2 + (-8) /2 = -3.
D’où : L (2 ; –3) .
▪ L et M , donc [BD] et [AC] se coupent en leur milieu ♦
.
b- Calculons AC et BD.
▪ AC² = (x
A – x
C )² + (y
A – y
C )² = (-3 –7)² + (-4 – (-2))² =
104.
D’où : AC =
104 = 2
26 .
▪ BD² = (x
B – x
D )² + (y
B – y
D )² = (3 – 1)² + (2 – (-8))² = 104.
D’où : BD =
104 = 2
26 .
▪ AC = BD, donc [BD] et [AC] sont de même longueur
♦♦
.
c - Calculons AB et CD.
A(-3 ; -4) ; B(3 ; 2) ; C(7 ; -2) et D(1 ;
-8)
▪ AB² = (x
A – x
B )² + (y
A – y
B )² = (-3 – 3)² + (-4 – 2)² = 72.
D’où : AB =
72 = 6
2 .
▪ CD² = (x
C – x
D )² + (y
C – y
D )² = (7 – 1)² + (-2 – (-8))² = 72.
D’où : CD =
72 = 6
2 .
▪ AB = CD, donc [AB] et [CD] sont de même longueur
♦ ♦♦
.
d - Conclusion .
ABCD est un rectangle.
En effet,
Propriété : Dans un rectangle,
▪ Les diagonales se coupent en leur milieu ♦
▪ Les diagonales sont de même longueur ♦♦
▪ Les côtés opposés ont même longueur ♦ ♦♦
.
4 - Calcul du rayon du cercle circonscrit à ABCD.
ABCD est un rectangle et M son centre de symétrie
qui est aussi centre du cercle circonscrit de rayon
MA = MB = MC = MD avec :
▪ MB = BD / 2 =
26 ou encore :
▪ MB² = (x
M – x
B )² + (y
M – y
B )² = (2 – 3)² + (-3 – 2)² = 26
D’où : MB =
26 .
Ex.
2 (8 pts)
1 - Choix du repère
orthonormé :
(D ; I , J)
Figure ci-contre.
2- Dans ce repère choisi, les coordonnées des points sont :
Point D A C B E
F
Coord.
(0 ; 0) (1 ; 4) (4 ; -1) (5 ; 3) (3 ; -5) (-
2 ; -5)
3- Coordonnées du point G milieu du segment [AE].
x
G = (x
A + x
E ) /2 = (1 + 3) /2 = 2
y
G = (y
A + y
E ) /2 = (4 + (-5) /2 = -1/2.
D’où : G (2 ; – 1
2 ) .
4 - Coordonnées du point H milieu du segment [BF].
x
H = (x
B + x
F ) /2 = (5 + (-2)) /2 = 3/2
y
H = (y
B + y
F ) /2 = (3 + (-5) /2 = -2/2 = -1.
D’où : H ( 3
2 ; –
1) .
Ex 106
Pixel 2de 2009 p173
1 a- Dans le repère orthonormé (A ; B, D), les
coordonnées
des points sont : A(0 ; 0) ; B(1 ; 0) ; C(1 ; 1) et D(0 ;
1).
b- Calcul de EH par Pythagore
2dC02_Repères-Coordonnées d’un Pt_DS03_Corrigé p 1/1 20.11.2014C H .
2 – R EPÈRES -C OORDONNÉES D ’ UN P OINT
C ONTRÔLE N°3 - C ORRIGÉ
S UJET 2
1,5 2
2
1,5 311
1
3
22 A
D
C B
EF IJ
xy
G
Hxy
DL B
A MO
IJ
C
1 BA C
D
FE
xy
H.
»
↓↓↓ APERÇU DU DOCUMENT ↓↓↓
Liens utiles
- La conscience de soi rend-elle libre ? (Corrigé) Problématisation
- HABERMAS, L’intégration républicaine, « Les droits de l’homme. À l’échelle mondiale et au niveau de l’État » (1996). Traduit de l’allemand par Rainer Rochlitz (revue) - corrigé HLP
- Corrigé Nietzsche Humain trop humain II
- Corrigé TP : SYNTHÈSE DE L’ASPIRINE
- Corrigé Commentaire de texte L’Illusion comique, Corneille, 1634