Le calcul différentiel

« sinus correspondant aux milieux considérés.

Comme Fermat l'avait remarqué , la détermination d 'un minimum (ou d'un maximum) se ramène à un calcul de tangente.

Pour l'exprimer plus précisément la tangente d'une courbe est « horizontale " en ses points extrêmes .

PASCAL ET LE TRIANGLE ARITHMÉTIQUE ,.,sc11/ a donné une impulsion décisive pour l'invention du calcul intégral, en étudiant les rapports réciproques entre différentes séries de nombres et ce qui en découle pour le calcul de la somme d 'un nombre quelconque de termes de ces séries.

C'est pour cette raison que Leibniz s'est intéressé au Traité du triangle arithmétique de Pascal.

Ce «triangle " a en réalité une base infinie.

Il s'agit d 'un ordonnancement d'une série de séries de nombres où l'on place tout d'abord, au sommet de ce triangle, un nombre quelconque , par exemple 1.

À droite de ce nombre , on dispose une infinité de 1 sur la même ligne.

On dispose ensuite sous le sommet une infinité de 1.

Pour remplir toutes les autres cases du triangle, on procède toujours de la même manière : le nombre inscrit dans une case est égal à la somme du nombre immédiatement au-dessus et du nombre immédiatement à gauche.

Il apparaît ainsi sur la seconde ligne, la série des nombres entiers : 1, 2, 3, 4, 5, 6 ...

Sur la troisième ligne , on obtient la série des nombres «triangulaires " : 1, 3, 6, 10, 15, 21 ..

.

Sur la quatrième ligne, on obtient la série des nombres «pyramidaux ": 1, 4, 10, 20, 35, 56 ...

Et ainsi de suite .

Il apparaît que ce triangle permet de donner immédiatement le résultat de la somme d'une série quelconque de termes consécutifs sur une ligne .

Pour cela, il suffit de faire la différence entre le terme de la ligne suivante de même rang que le dernier terme de la série , et le terme de la ligne suivante de rang immédiatement inférieur que le premier terme de la série (si le premier terme de la série vaut 1, on prendra 0 pour le terme correspondant).

Par exemple , en utilisant la cinquième et la sixième ligne du triangle , on peut vérifier que 15 + 35 + 70 + 126 est égal à la différence 252 -6, c'est -à-dire 246.

Il en résulte qu'une somme d 'un nombre de termes aussi grand que l'on veut peut se calculer par une simple différence de deux nombres .

S'inspirant de cette découverte de Pascal, Leibniz montrera par la suite que l'on peut même calculer des sommes infinies par des procédés du même type .

Construisant ce qu'il appelle le « triangle harmonique " obtenu en inversant tous les termes du « triangle de Pascal "· leibniz montre que : 1/1 + 1/3 + 1/6 + 1/10 + 1/15 + ...

= 2/1 1/1 + 1/4 + 1/10 + 1/20 + 1/35 + ...

= 3 / 2 1/1 + 1/5 + 1/15 + 1/35 + 1/70 + ...

= 4 /3 Et ainsi de suite .

Par ailleurs , ces triangles suggèrent à Leibniz que les opérations de somme (calcul intégral) et de différence (calcul différentiel) sont réciproques l'une de l'autre .

L'APPORT DE LEIBNIZ LA NOTATION Si l 'on considère un certain ensemble de variables mathématiques x, y , z, etc., on peut associer à chacune des quantités infinitésimales- ou « plus petites que n 'importe quelle valeur donnée " - que l'on note en utilisant le préfi x e « d "· ce qui donne : dx, dy, dz, etc.

Ceci étant posé , Leibniz énonce un certain nombre de règles de différentiation.

Les plus connues sont : d(x + y) = dx + dy d(A} = o (si A est une constante ) d(xy) = xdy + ydx d(1/x) =- dxfxx l'expression mathématique d 'une courbe étant donnée, il devient alors possible de calculer directement sa tangente en un point quelconque : il suffit de différentier l'expression de la courbe.

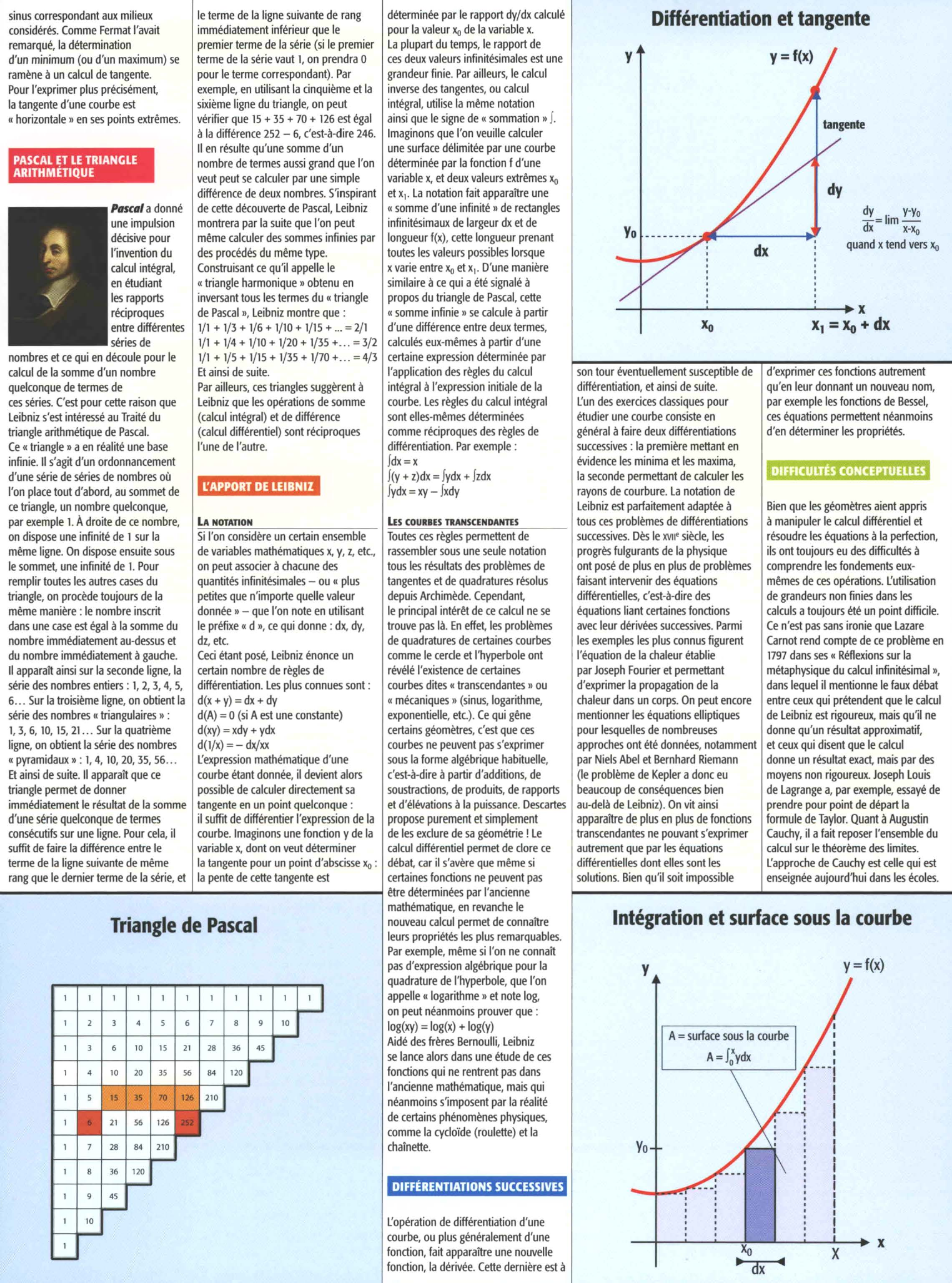
Imaginons une fonction y de la variable x, dont on veut déterminer la tangente pour un point d'ab scisse x, : la pente de cette tangente est déterminée par le rapport dy/dx calculé pour la valeur x, de la variable x .

la plupart du temps , le rapport de ces deux valeurs infinitésimales est une grandeur finie .

Par ailleurs , le calcul inverse des tangentes , ou calcul intégral.

utilise la même notation ainsi que le signe de « sommation "I.

Imaginons que l'on veuille calculer une surface délimitée par une courbe déterminée par la fonction f d 'une variable x, et deux valeurs extrêmes x, et x,.

La notation fait apparaître une « somme d'une infinité " de rectangles infinitésimaux de largeur dx et de longueur f(x), cette longueur prenant toutes les valeurs possibles lorsque x varie entre Xo et x1• D'une manière similaire à ce qui a été signalé à propos du triangle de Pascal, cette « somme infinie " se calcule à partir d 'une différence entre deux termes , calculés eux-mêmes à partir d 'une certaine expression déterminée par l'application des règles du calcul intégral à l 'expression initiale de la courbe .

Les règle s du calcul intégral sont elles-mêmes déterminées comme réciproques des règles de différentiation .

Par exemple : J dx=x J (y + z)dx = Jydx + Jzdx Jydx = xy- Jxdy Lfs COUIBES TIANSCENDANTES Toutes ces règles permettent de rassembler sous une seule notation tous les résultats des problèmes de tangentes et de quadratures résolus depuis Archimède .

Cependant le principal intérêt de ce calcul ne se trouve pas là.

En effet les problèmes de quadratures de certaines courbes comme le cercle et l'hyperbole ont révélé l'existence de certaines courbes dites « transcendantes " ou « mécaniques " (sinus, logarithme, exponentielle, etc.) .

Ce qui gêne certains géomètres, c'est que ces courbes ne peuvent pas s 'exprimer sous la forme algébrique habituelle, c'est -à-dire à partir d'additions , de soustractions , de produits , de rapports et d'élévations à la puissance.

Descartes propose purement et simplement de les exclure de sa géométrie ! le calcul différentiel permet de clore ce débat , car il s'avère que même si certaines fonctions ne peuvent pas ------------....1.-------------l être déterminées par l'ancienne Triangle de Pascal mathématique, en revanche le nouveau calcul permet de connaître leurs propriétés les plus remarquables .

Par exemple , même si l'on ne connaît pas d'expression algébrique pour la quadrature de l'hyperbole , que l 'on appelle « logarithme " et note log.

on peut néanmoins prouver que : log(xy) = log(x) + log(y) Aidé des frères Bernoulli, Leibniz se lance alors dans une étude de ces fonctions qui ne rentrent pas dans l'ancienne mathématique, mais qui néanmoins s 'imposent par la réalité de certains phénomènes physiques , comme la cycloïde (roulette) et la chaînette.

DIFFÉRENTIATIONS SUCCESSIVES l'opération de différentiation d 'une courbe, ou plus généralement d'une fonction, fait apparaître une nouvelle fonction, la dérivée.

Cette dernière est à Différentiation et tangente y ~=lim Y·Yo dx x-x, quand x tend vers Xo --;-----~~--------~---.x son tour éventuellement susceptible de différentiation , et ainsi de suite .

l'un des exercices classiques pour étudier une courbe consiste en général à faire deux différentiations succes sives : la première mettant en évidence les minima et les maxima , la seconde permettant de calculer les rayons de courbure.

la notation de Leibniz est parfaitement adaptée à tous ces problèmes de différentiations successives .

Dès le XVI~ siècle , les progrés fulgurants de la physique ont posé de plus en plus de problèmes faisant intervenir des équations différentielles , c'est-à-dire des équations liant certaines fonctions avec leur dérivées succes sives.

Parmi les exemples les plus connus figurent l'équation de la chaleur établie par Joseph Fourier et permettant d'exprimer la propagation de la chaleur dans un corps .

On peut encore mentionner les équations elliptiques pour lesquelles de nombreuses approches ont été données , notamment par Niels Abel et Bernhard Riemann (le problème de Kepler a donc eu beaucoup de conséquences bien au-delà de leibniz) .

On vit ainsi apparaître de plus en plus de fonctions transcendantes ne pouvant s 'exprimer autrement que par les équations différentielles dont elles sont les solutions .

Bien qu'il soit impossible x1 =Xo + dx d'exprimer ces fonctions autrement qu'en leur donnant un nouveau nom, par exemple les fonctions de Bessel, ces équations permettent néanmoins d 'en déterminer les propriétés .

DIFFICULTES CONCEPTUELLES Bien que les géomètres aient appris à manipuler le calcul différentiel et résoudre les équations à la perfection, ils ont toujours eu des difficultés à comprendre les fondements eux­ même s de ces opérations .

L'utilisation de grandeurs non finies dans les calculs a toujours été un point difficile .

Ce n'est pas sans ironie que lazare Carnot rend compte de ce problème en 1797 dans ses « Réflexions sur la métaphysique du calcul infinitésimal "· dans lequel il mentionne le faux débat entre ceux qui prétendent que le calcul de Leibniz est rigoureux , mais qu'il ne donne qu'un résultat approximatif , et ceux qui disent que le calcul donne un résultat exact mais par des moyens non rigoureux .

Joseph Louis de lagrange a, par exemple, essayé de prendre pour point de départ la formule de Taylor.

Quant à Augustin Cauchy, il a fait reposer l'ensemble du calcul sur le théorème des limites .

l'approche de Cauchy est celle qui est enseignée aujourd'hui dans les écoles.

Intégration et surface sous la courbe y y= f(x) Yo x. »