Intégrales

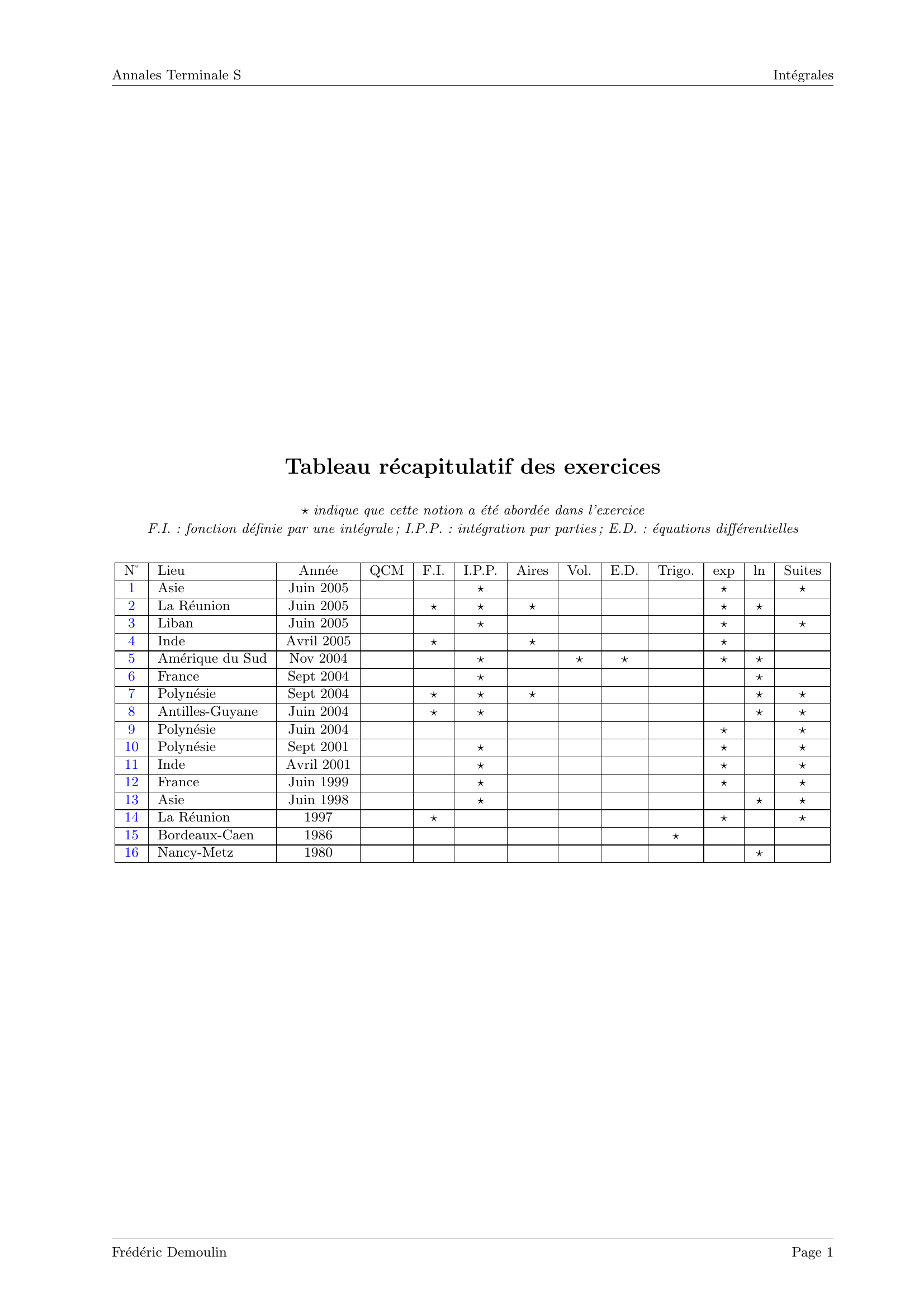
´ Recueil d'annales en Mathematiques Terminale S - Enseignement obligatoire ´ Integrales Fr´d´ric Demoulin1 ee Derni`re r´vision : 16 septembre 2005 e e 1 [email protected] Annales Terminale S Int´grales e Tableau r´capitulatif des exercices e ? indique que cette notion a ´t´ abord´e dans l'exercice ee e F.I. : fonction d´finie par une int´grale ; I.P.P. : int´gration par parties ; E.D. : ´quations diff´rentielles e e e e e N ? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Lieu Asie La R´union e Liban Inde Am´rique du Sud e France Polyn´sie e Antilles-Guyane Polyn´sie e Polyn´sie e Inde France Asie La R´union e Bordeaux-Caen Nancy-Metz Fr´d´ric Demoulin ee Ann´e e Juin 2005 Juin 2005 Juin 2005 Avril 2005 Nov 2004 Sept 2004 Sept 2004 Juin 2004 Juin 2004 Sept 2001 Avril 2001 Juin 1999 Juin 1998 1997 1986 1980 QCM F.I. ? I.P.P. ? ? ? ? ? ? Aires Vol. E.D. Trigo. ? ? ? ? ? ? ? ? exp ? ? ? ? ? ? ln ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? Suites ? ? ? ? ? ? ? ? ? ? ? ? Page 1 Annales Terminale S Int´grales e Exercice 1 Asie, Juin 2005 (7 points) On s'int´resse dans cet exercice ` une suite de nombres rationnels qui converge vers e2 . e a On d´finit, pour tout entier naturel n 1, l'int´grale : e e 2 In = 0 1 (2 - x)n ex dx. n! 1. Calculer I1 . 2n 2 e -1 . n! ` 3. A l'aide d'une int´gration par parties, montrer que pour tout entier naturel n e ´ 2. Etablir que pour tout entier naturel n 1, 0 In In+1 = In - 1: 2n+1 . (n + 1)! 2n 2 22 + + ... + + In . 1! 2! n! 2n 1, un = . n! 4. D´montrer par r´currence que e2 = 1 + e e 5. On pose, pour tout entier naturel n (a) Calculer un+1 et prouver que pour tout entier naturel n un (b) En d´duire que pour tout entier naturel n e 3, 0 3, un+1 un u3 1 un . 2 n-3 1 2 . 6. En d´duire la limite de la suite (un ) puis celle de la suite (In ). e 7. Justifier enfin que : e2 = lim n->+? Exercice 2 1+ 2 22 2n + + ... + 1! 2! n! La R´union, Juin 2005 e . (3 points) L'exercice comporte une annexe a rendre avec la copie. ` On consid`re les fonctions f et g d´finies, sur l'intervalle [0 ; +?[, par : e e f (x) = ln(x + 1) et g (x) = ex - 1. On d´signe par Cf et Cg les courbes repr´sentatives des fonctions f et g dans un rep`re orthonormal e e e ->-> (O ; - , - ). Ces courbes sont trac´es sur la feuille annexe, dont le candidat disposera comme il le jugera ?? e utile ; cette annexe sera ` joindre ` la copie, avec les ´ventuels ajouts effectu´s par le candidat. a a e e 1. V´rifier que les courbes Cf et Cg ont une tangente commune au point O(0 ; 0). Pr´ciser la position de e e la courbe Cf par rapport ` cette tangente. a 2. D´montrer que les courbes Cf et Cg sont sym´triques par rapport ` la droite d'´quation y = x. e e a e 3. Soit a un nombre r´el strictement positif. On se propose de calculer de deux fa¸ons diff´rentes le e c e a ln(x + 1) dx. nombre I (a) = 0 (a) En utilisant des consid´rations d'aires, d´montrer que : e e ln(a+1) I (a) = a ln(a + 1) - Fr´d´ric Demoulin ee 0 (ex - 1) dx. Page 2 Annales Terminale S Int´grales e (b) En d´duire la valeur de I (a). e (c) Retrouver la valeur de I (a) en effectuant une int´gration par parties. e Annexe (` rendre avec la copie) a 4 3 2 1 0 0 1 Exercice 3 2 3