Grand oral du bac : LA TRIGONOMÉTRIE
Publié le 04/02/2019

Extrait du document
La trigonométrie sphérique
La trigonométrie sphérique a pour objet les triangles sphériques, c’est-à-dire les triangles délimités par des arcs de cercles tracés sur la surface d’une sphère. De même que le triangle plan, le triangle sphérique est caractérisé par six éléments: ses trois angles et la longueur de ses trois côtés courbes. Des formules mathématiques relient les paramètres entre eux. La trigonométrie sphérique est surtout utilisée en astronomie et en navigation.
La trigonométrie permet également de déterminer les relations entre les côtés et les angles d’un triangle quelconque. Considérons un triangle quelconque dont les trois angles sont désignés par les lettres A, B, C, opposés respectivement aux côtés de longueur a, b et c. On a alors les relations suivantes :
On peut utiliser ces relations pour déterminer les six éléments du triangle (les trois longueurs et les trois angles). Le procédé de triangulation, introduit par l’astronome danois Tycho Brahé (1546-1601) à la fin du xvie siècle, utilise la première relation. Le principe est le suivant: si l’on connaît, dans un triangle, les angles A et B (on connaît donc C, car la somme des angles d’un triangle plan est égal à 180°) et le côté c, alors on peut déterminer les côtés a et b. Le principe de triangulation est utilisé en géodésie pour tracer la carte d’une région.
«
La
trigonométrie
unité de mesure des angles.
Un radian corres
pond à la mesure de l'angle qui intercepte, sur la
circonférence du cercle, un arc de cercle de lon
gueur égale au rayon du cercle.
On a ainsi les
équivalences suivantes:
36 0° = 2n rad; 180° = 1t rad; 1 o = n/180 rad.
En trigonométrie, un angle est représenté par
une grandeur algébrique, c'est-à-dire par un
nombre positif ou négatif; il s'agit d'un angle
orienté.
Pour cela, on choisit, dans le plan orien
té, un sens positif de rotation, généralement le
sens invers e de rotation des aiguilles d'une
montre.
Considérons la figure suivante:
.
..
......
......
.
.
.
.
.
..
.
· ·· · ·
.
.
.
.
.
.
.
.
.
.
.
.
.
.
· .
.
• ..
..
--....
....
.
··
.
.
· .
.
.
' .
.
.
.
.
.
..:::::;-:::::.
La mesure de l'angle a [angle noté (OA,OB)]
correspond à l'angle de rotation qu'il faut appli
quer à (OA ) pour l'amener sur (OB).
Ici, la rota
tion s'effectue dans le sens positif, donc a est
positif.
Dans le cas contraire, a aurait été négatif.
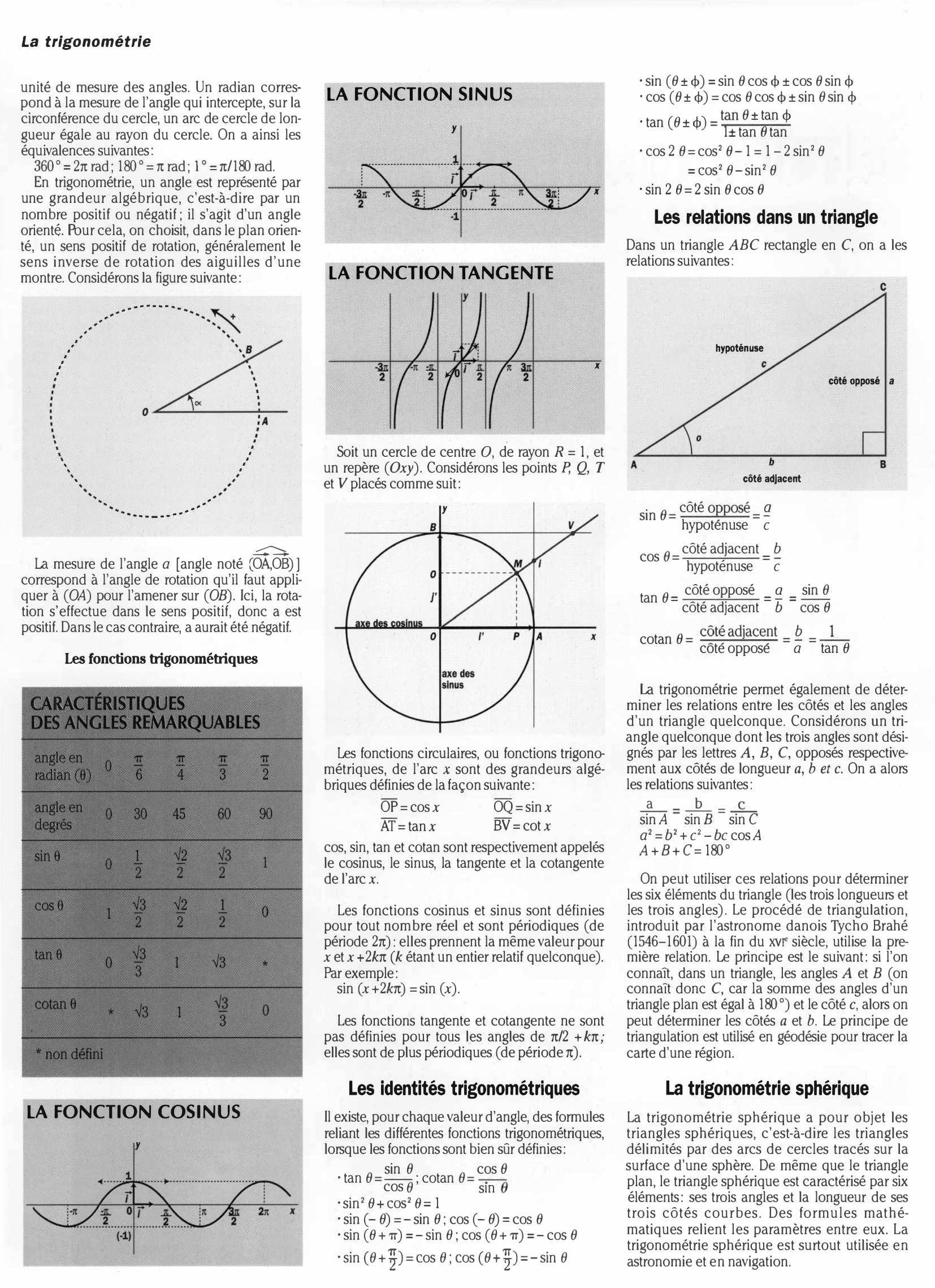
Les fonctions trigonométriques
LA FONCTION COSINUS
1 LA
FONCTION SINUS
1
JI
LA FONCTION TANGENTE
JI
Soit un cercle de centre 0, de rayon R = 1, et
un repère (Oxy).
Considérons les points P, Q, T
et V placés comme suit:
1
Les fonctions circulaires, ou fonctions trigono
métriques, de l'arc x sont des grandeurs algé
briques définies de la façon suivante:
OP=cosx OQ=sinx
AT= tan x BV
= cot x
cos, sin, tan et cotan sont respectivement appelés
le cosinus, le sinus, la tangente et la cotangente
de l'arc x.
Les fonctions cosinus et sinus sont définies
pour tout nombre réel et sont périodiques (de
période 2n): elles prennent la même valeur pour
x et x +2kn (k étant un entier relatif quelconque).
Par exemple:
sin (x+2kn) =sin (x).
Les fonctions tangente et cotangente ne sont
pas définies pour tous les angles de n/2 +kn;
elles sont de plus périodiques (de période 1t).
Les identités trigonométriques
Il existe, pour chaque valeur d'angle, des formules
reliant les différentes fonctions trigonométriques,
lorsque les fonctions sont bien sûr définies:
sin 8 cos 8
· tan 8 = -- 8; cotan 8 =
-.- 8
cos sm
· sin2 8+COS2 8= 1
· sin (-8) =- sin 8 ; cos (-8) = cos 8
·sin (8 +'TT )=- sin 8; cos (8+ 'TT)=- cos 8
·sin ( 8 + ;) =cos 8 ; cos ( 8 + ;) =-sin 8 ·sin
( 8 ± ) =sin 8 cos ±cos 8 sin
· cos ( 8 ± ) = cos 8 cos ±sin 8 sin
.
tan ( 8 ± ) =
tan 8
±tan
1±tan Otan
·cos 2 8= cos2 8-1 = 1- 2 sin2 8
=COS2 8-sin2 8
· sin 2 8 = 2 sin 8 cos 8
Les relations dans un triangle
Dans un triangle ABC rectangle en C, on a les
relations suivantes:
A c
hypoténuse côté opposé a
b
côté adjacent
sin 8 = côté oppo
sé
= Q
hypotenuse c
8 côté adJ·acent b
cos =
•
hypotenuse c
tan 8 =
côté opposé = q_ = sin 8
côté adjacent b cos 8
cotan 8 = c
� t� adjace
�t
= � = _1
_
cote
oppose a tan 8 B
La trigonométrie permet également de déter
miner les relations entre les côtés et les angles
d'un triangle quelconque.
Considérons un tri
angle quelconque dont les trois angles sont dési
gnés par les lettres A, B, C, opposés respective
ment aux côtés de longueur a, b et c.
On a alors
les relations suivantes:
a ___Q_ = _c_
sin A
sin B sin C
a2 = b2 + c2-be cos A
A +B+C= 180°
On peut utiliser ces relations pour déterminer
les six éléments du triangle (les trois longueurs et
les trois angles).
Le procédé de triangulation,
introduit par l'astronome danois Tycho Brahé
(1546-1601) à la fin du xv1• siècle, utilise la pre
mière relation.
Le principe est le suivant: si l'on
connaît, dans un triangle, les angles A et B (on
connaît donc C, car la somme des angles d'un
triangle plan est égal à 180°) et le côté c, alors on
peut déterminer les côtés a et b.
Le principe de
triangulation est utilisé en géodésie pour tracer la
carte d'une région.
La trigonométrie sphérique
La trigonométrie sphérique a pour objet les
triangles sphériques, c'est-à-dire les triangles
délimités par des arcs de cercles tracés sur la
surface d'une sphère.
De même que le triangle
plan, le triangle sphérique est caractérisé par six
éléments: ses trois angles et la longueur de ses
trois côtés courbes.
Des formules mathé
matiques relient les paramètres entre eux.
La
trigonométrie sphérique est surtout utilisée en
astronomie et en navigation..
»
↓↓↓ APERÇU DU DOCUMENT ↓↓↓
Liens utiles
- Grand oral du bac : Arts et Culture L'ART DE LA PHOTOGRAPHIE
- Grand oral du bac : Arts et Culture LE BAUHAUS
- Grand oral du bac : Arts et Culture LE BAROQUE
- Grand oral du bac : WALT DISNEY
- Grand oral du bac : GEORGE ORWELL