exercice maths corrige

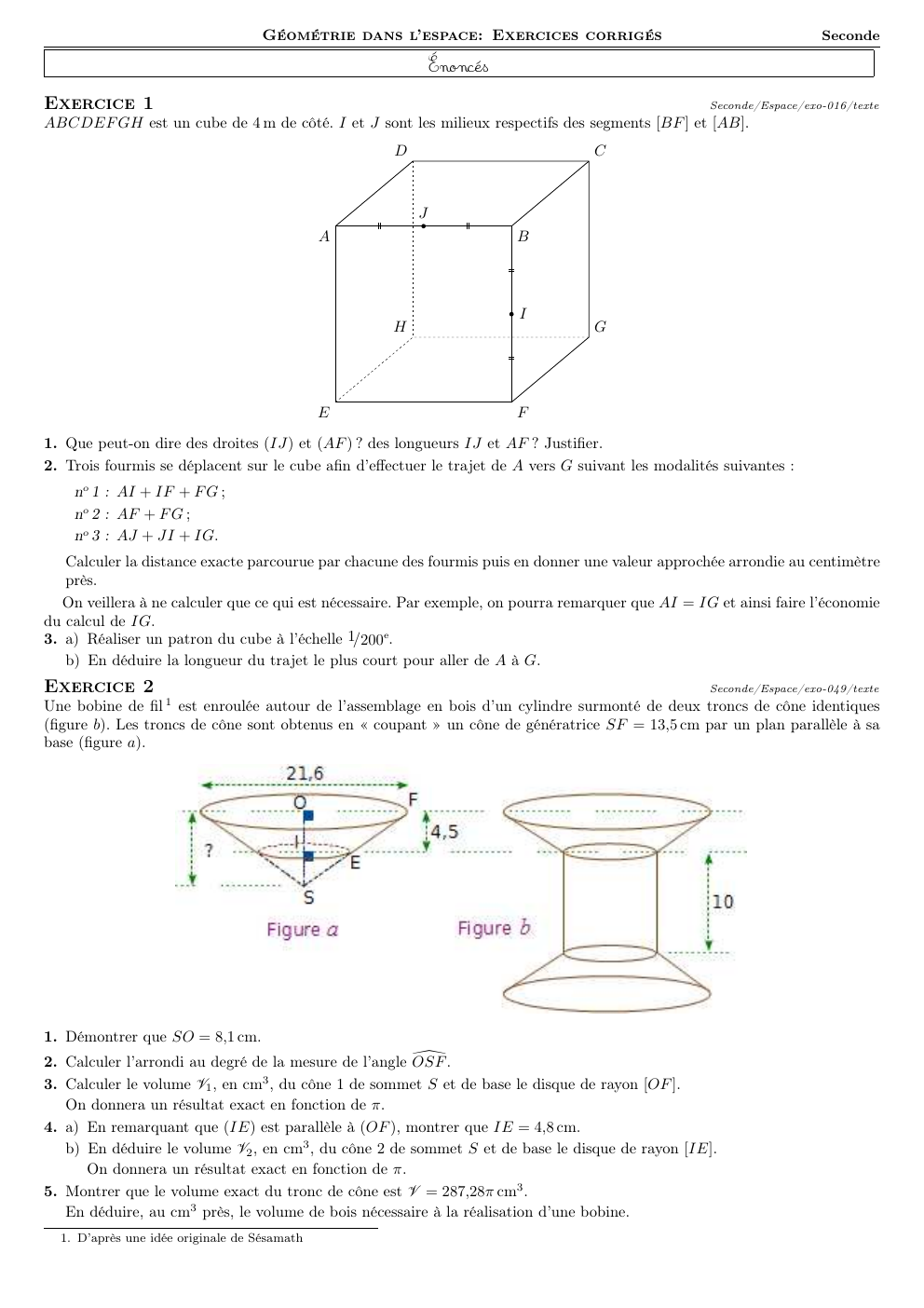
« Géométrie dans l’espace: Exercices corrigés Seconde ɕn€o”n€ éš Exercice 1 Seconde/Espace/exo-016/texte ABCDEF GH est un cube de 4 m de côté.

I et J sont les milieux respectifs des segments [BF ] et [AB]. D C J A B H E I G F 1.

Que peut-on dire des droites (IJ) et (AF ) ? des longueurs IJ et AF ? Justifier. 2.

Trois fourmis se déplacent sur le cube afin d’effectuer le trajet de A vers G suivant les modalités suivantes : no 1 : AI + IF + F G ; no 2 : AF + F G ; no 3 : AJ + JI + IG. Calculer la distance exacte parcourue par chacune des fourmis puis en donner une valeur approchée arrondie au centimètre près. ✎ On veillera à ne calculer que ce qui est nécessaire.

Par exemple, on pourra remarquer que AI = IG et ainsi faire l’économie du calcul de IG. 3.

a) Réaliser un patron du cube à l’échelle 1/200e. b) En déduire la longueur du trajet le plus court pour aller de A à G. Exercice 2 Seconde/Espace/exo-049/texte Une bobine de fil 1 est enroulée autour de l’assemblage en bois d’un cylindre surmonté de deux troncs de cône identiques (figure b).

Les troncs de cône sont obtenus en « coupant » un cône de génératrice SF = 13,5 cm par un plan parallèle à sa base (figure a). 1.

Démontrer que SO = 8,1 cm. ’. 2.

Calculer l’arrondi au degré de la mesure de l’angle OSF 3 3.

Calculer le volume V1 , en cm , du cône 1 de sommet S et de base le disque de rayon [OF ]. On donnera un résultat exact en fonction de π. 4.

a) En remarquant que (IE) est parallèle à (OF ), montrer que IE = 4,8 cm. b) En déduire le volume V2 , en cm3 , du cône 2 de sommet S et de base le disque de rayon [IE]. On donnera un résultat exact en fonction de π. 5.

Montrer que le volume exact du tronc de cône est V = 287,28π cm3 . En déduire, au cm3 près, le volume de bois nécessaire à la réalisation d’une bobine. 1.

D’après une idée originale de Sésamath Exercice 3 Géométrie dans l’espace: Exercices corrigés S Sur la figure ci-contre, on a représenté en perspective cavalière une pyramide à base carrée SABCD de hauteur [SA]. Le triangle SAB est rectangle en A, AB = 9 cm et SA = 12 cm. EF GH est la section de la pyramide SABCD par le plan parallèle à la base et telle que SE = 4 cm Seconde Seconde/Espace/exo-050/texte H E G F 1.

Donner la liste des segments qui devraient être représentés en pointillés sur la figure. 2.

a) Calculer SB. b) Démontrer que EF = 3 cm. 3.

Calculer le volume du tronc de pyramide ABCDEF GH. C 1 ✎ On rappelle que le volume d’une pyramide est donné par V = × B × h 3 où B et h désignent respectivement l’aire de la base et la hauteur de la pyramide. D A B Géométrie dans l’espace: Exercices corrigés Seconde C€oŠrˆrˆi€géš Exercice 1 Seconde/Espace/exo-016/corrige 1.

Théorème de la droite des milieux : Si un segment a pour extrémités les milieux de deux des trois côtés d’un triangle alors il est parallèle au troisième côté et sa longueur est égale à la moitié de celle de ce troisième côté. Dans le triangle ABF , I est le milieu de [BF ] et J le milieu de [AB] donc les droites.... »