document

« Exercice1 Soit dans un rep`ere les points A(− 1; 1), B(2; 3), C(− 2; −4) et D(1; −2). Montrer de deux mani`eres diff´erentes que le quadrilat`ere ABDCest un parall´elogramme. Exercice 2 Soit dans un rep`ere A(2; 3), B(− 5; 7) et C(3; −12). D´eterminer les coordonn´ees des vecteurs −→ AB ,−−→ BC ,−→ AC , et ~u= −→ AB +−−→ BC . Que retrouve-t-on ? Propri´et´e Equation r´eduite d’une droite Toute droite Dnon paral l`ele `a l’axe des ordonn´ees admet une ´equation d e la forme y = ax +bo`u aet bsont deux nombres r´eels, • le point A(0; b) est toujours sur la droite D;b s’appel le l’ordonn´ee `a l’origine de la droite D. • Lorsque xaugmente de 1, y varie de a;a s’appel le le coefficient directeur de la droite. Remarque : Toute droite d’´equation y= ax +best la repr´esentation graphique de la fonction affine f (x ) = ax+b. Les points de C f sont les points M(x ;y ) tels que y= f(x ), soit y= ax +b. 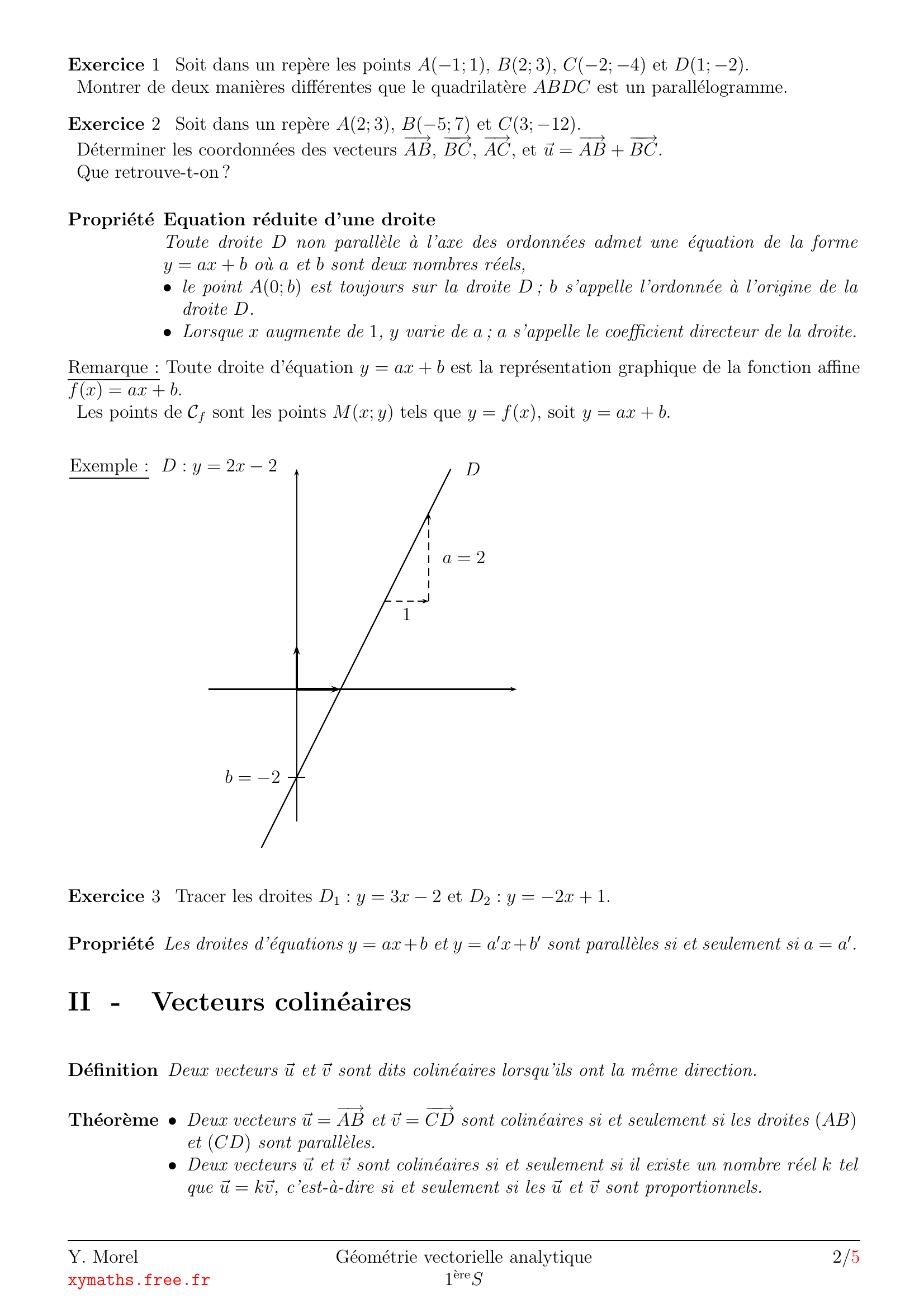Exemple : D :y = 2 x− 2 D 1 a= 2 b= −2 Exercice 3 Tracer les droites D 1: y = 3 x− 2 et D 2: y = −2x + 1. Propri´et´e Les droites d’´equations y= ax +bet y= a′ x + b′ sont paral l`eles si et seulement si a= a′ . II - Vecteurs colin´eaires D´efinition Deux vecteurs ~uet ~vsont dits colin´eaires lorsqu’ils ont la mˆeme direction. Th´eor`eme •Deux vecteurs ~u= −→ AB et~v= −−→ C D sont colin´eaires si et seulement si les droites (AB ) et (C D )sont paral l`eles. • Deux vecteurs ~uet ~vsont colin´eaires si et seulement si il existe un nombre r´ee lk tel que ~u= k~v, c’est-`a-dire si et seulement si les ~uet ~vsont proportionnels. Y.

Morel xymaths.free.fr G´eom´etrie vectorielle analytique 1`ere S 2/ 5. »