Corrigé Probabilité

« Mercatique, comptabilité et finance d’entreprise gestion des systèmes d’informationA.

P.

M.

E.

P. EX E R C I C E 2 5 points Le tableau ci-dessous retrace l’évolution sur vingt ans du r ecord du monde du 100 m en athlétisme chez les hommes. Année Rang de l’année¡ x i¢ Temps en seconde ¡ y i¢ Carl Lewis 1988 0 9,92 Carl Lewis 1991 3 9,86 Leroy Burrell 1994 6 9,85 Donovan Bailey 1996 8 9,84 Maurice Greene 1999 11 9,79 Asafa Powell 2005 17 9,77 Asafa Powell 2007 19 9,74 Usain Bolt 2008 20 9,69 1.

a. Calculons le taux d’évolution du temps du record du monde du 1 00 m en athlétisme chez les hommes entre 1988 et 2008.

Le taux est défini par valeur finale −valeur initiale valeur initiale . T = 9,69 −9,92 9,92 ≈ − 0,023 2. Entre 1988 et 2008, le temps du record du monde mis pour courir le 100 m a baissé de 2,32 %. b.

Sur les 20 années de 1988 à 2008, montrons que le temps du recor d du monde à l’épreuve du 100 m en athlétisme chez les hommes a baissé chaque année en moyenne d e 0,117 %. Entre 1988 et 2008, le temps du record a subi 20 évolutions au t aux moyen annuelt m , le coefficient multi- plicateur associé est donc (1 + t m )20 d’une part et de 1 −0,023 2 =0,976 8 d’autre part. Par conséquent, t m = (0,976 8 )1 20 −1≈ − 0,001 17 soit environ 0,117 %. 2.

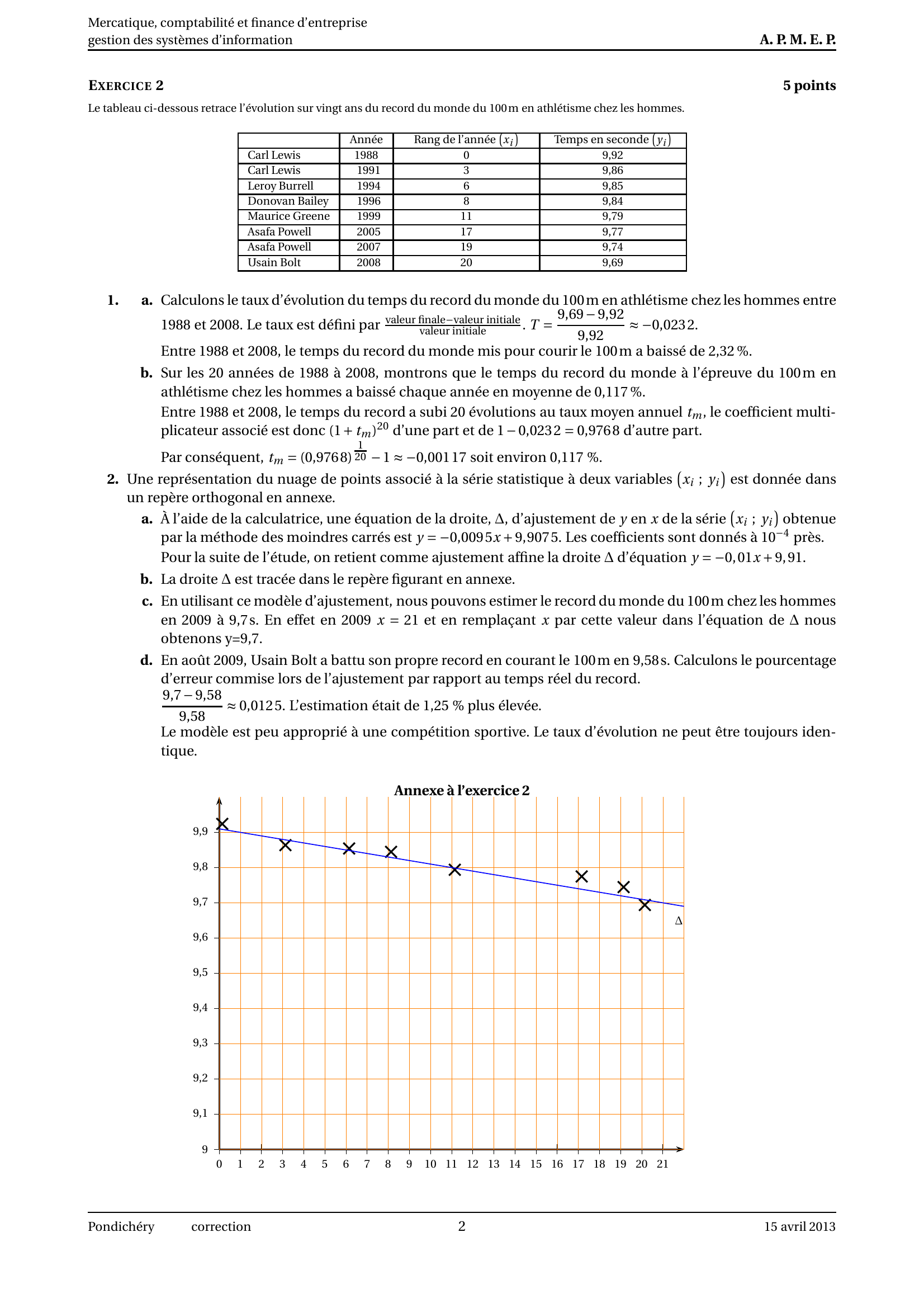
Une représentation du nuage de points associé à la série stat istique à deux variables¡ x i ; y i¢ est donnée dans un repère orthogonal en annexe. a.

À l’aide de la calculatrice, une équation de la droite, ∆, d’ajustement de yen xde la série ¡ x i ; y i¢ obtenue par la méthode des moindres carrés est y= − 0,009 5 x+ 9,907 5.

Les coefficients sont donnés à 10 − 4 près. Pour la suite de l’étude, on retient comme ajustement affine l a droite∆d’équation y= − 0, 01 x+ 9, 91. b.

La droite ∆est tracée dans le repère figurant en annexe. c.

En utilisant ce modèle d’ajustement, nous pouvons estimer l e record du monde du 100 m chez les hommes en 2009 à 9,7 s.

En effet en 2009 x= 21 et en remplaçant xpar cette valeur dans l’équation de ∆nous obtenons y=9,7. d.

En août 2009, Usain Bolt a battu son propre record en courant l e 100 m en 9,58 s.

Calculons le pourcentage d’erreur commise lors de l’ajustement par rapport au temps r éel du record. 9,7 −9,58 9,58 ≈ 0,012 5.

L’estimation était de 1,25 % plus élevée. Le modèle est peu approprié à une compétition sportive.

Le ta ux d’évolution ne peut être toujours iden- tique. Annexe à l’exercice 2 9 9,1 9,2 9,3 9,4 9,5 9,6 9,7 9,8 9,9 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 × ×× × × × × × ∆ Pondichéry correction 215 avril 2013. »