brevet

« 2 1) Montrer que, si on choisit le nombre 2, le résultat obtenu est 20.

(0,5 pt) 2) Calculer la valeur exacte du résultat lorsque :  Le nombre choisit est –2.

(0,5 pt)  Le nombre choisit est 3 2.

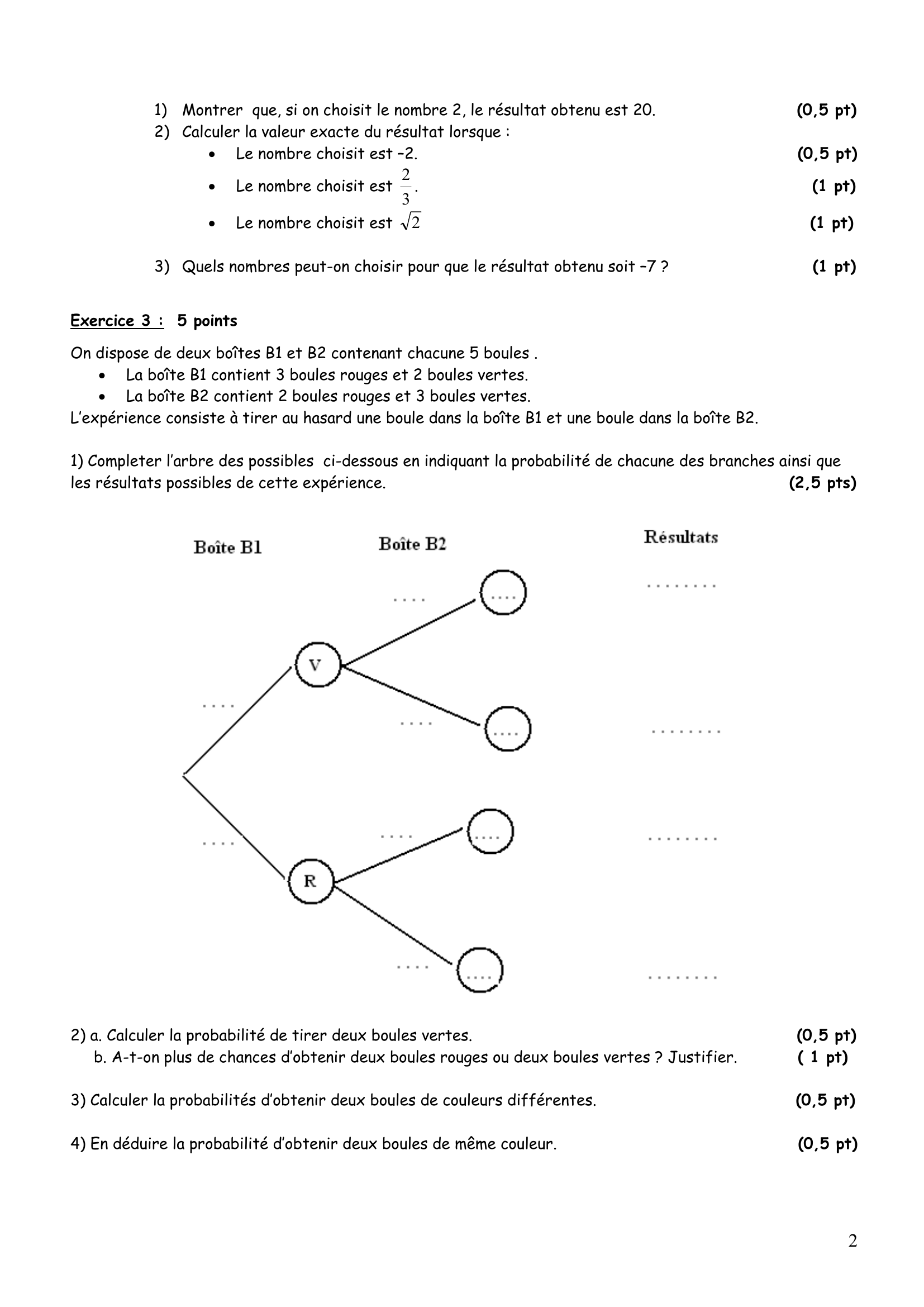
(1 pt)  Le nombre choisit est 2 (1 pt) 3) Quels nombres peut-on choisir pour que le résultat obtenu soit –7 ? (1 pt) Exercice 3 : 5 points On dispose de deux boîtes B1 et B2 contenant chacune 5 boules .

 La boîte B1 contient 3 boules rouges et 2 boules vertes.

 La boîte B2 contient 2 boules rouges et 3 boules vertes.

L’expérience consiste à tirer au hasard une boule dans la boîte B1 et une boule dans la boîte B2.

1) Completer l’arbre des possibles ci-dessous en indiquant la probabilité de chacune des branches ainsi que les résultats possibles de cette expérience.

(2,5 pts) 2) a.

Calculer la probabilité de tirer deux boules vertes.

(0,5 pt) b.

A-t-on plus de chances d’obtenir deux boules rouges ou deux boules vertes ? Justifier.

( 1 pt) 3) Calculer la probabilités d’obtenir deux boules de couleurs différentes.

(0,5 pt) 4) En déduire la probabilité d’obtenir deux boules de même couleur.

(0,5 pt). »