- 1 -dériv°cours1°S-version remp.

- 1 -dériv°cours1°S-version remp.doc 1°S- programme 2010 DERIVEE D’UNE FONCTION Activité photocopiée : découverte nombre dérivé I. Nombre dérivé d’une fonction f en un point a : 1 – Taux d’accroissement déf : Soit f une fonction définie sur un intervalle I, a et a + h deux nombres distincts de I. On appelle taux d’accroissement de f entre a et a + h (ou taux de variation) le quotient : f(a + h) – f(a) , avec h ? 0 h Exemples : 1. voir activité : d (t ) ? 4,9t ² . le taux d’accroissement entre 2 et 2+h est : d (2 ? h) ? d (2) 4,9(2 ? h)² ? 4,9 ? 2² 4,9(4 ? 4h ? h²) ? 4,9 ? 4 19.6h ? 4,9h² ? ? ? ? 19,6 ? 4,9h h h h h 2. f ( x) ? x 3 Taux d’accroissement entre 1 et 1+h : f (1 ? h) ? f (1) (1 ? h) 3 ? 13 (1 ? h)(1 ? h)² ? 1 (1 ? h)(1 ? 2h ? h²) ? 1 1 ? 2h ? h² ? h ? 2h² ? h 3 ? 1 3h ? 3h² ? h 3 ? ? ? ? ? ? 3 ? 3h ? 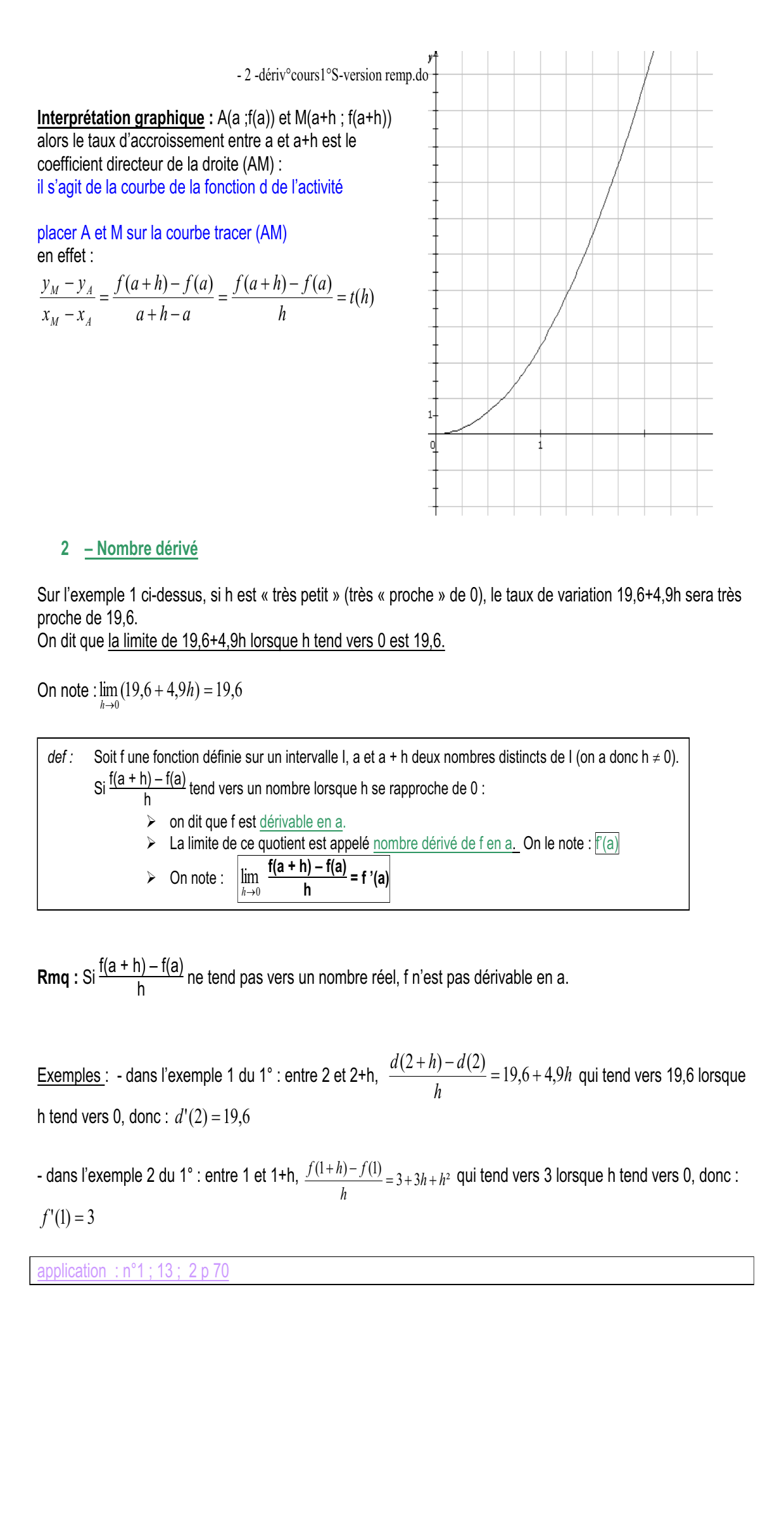h² h h h h h h - 2 -dériv°cours1°S-version remp.doc Interprétation graphique : A(a ;f(a)) et M(a+h ; f(a+h)) alors le taux d’accroissement entre a et a+h est le coefficient directeur de la droite (AM) : il s’agit de la courbe de la fonction d de l’activité placer A et M sur la courbe tracer (AM) en effet : yM ? y A f ( a ? h) ? f ( a ) f ( a ? h) ? f ( a ) ? ? ? t ( h) xM ? x A a?h?a h 2 – Nombre dérivé Sur l’exemple 1 ci-dessus, si h est « très petit » (très « proche » de 0), le taux de variation 19,6+4,9h sera très proche de 19,6. On dit que la limite de 19,6+4,9h lorsque h tend vers 0 est 19,6. On note : lim (19,6 ? 4,9h) ? 19,6 h ?0 def : Soit f une fonction définie sur un intervalle I, a et a + h deux nombres distincts de I (on a donc h ? 0). f(a + h) – f(a) Si tend vers un nombre lorsque h se rapproche de 0 : h ? on dit que f est dérivable en a. ? La limite de ce quotient est appelé nombre dérivé de f en a. On le note : f’(a) f(a + h) – f(a) ? On note : lim = f ’(a) h h?0 Rmq : Si f(a + h) – f(a) ne tend pas vers un nombre réel, f n’est pas dérivable en a. h Exemples : - dans l’exemple 1 du 1° : entre 2 et 2+h, h tend vers 0, donc : d ' (2) ? 19,6 d (2 ? h) ? d (2) ? 19,6 ? 4,9h qui tend vers 19,6 lorsque h - dans l’exemple 2 du 1° : entre 1 et 1+h, f (1 ? h) ? f (1) ? 3 ? 3h ? h² qui tend vers 3 lorsque h tend vers 0, donc : f ' (1) ? 3 application : n°1 ; 13 ; 2 p 70 h - 3 -dériv°cours1°S-version remp.doc II. Nombre dérivé et tangente : Interprétation géométrique du nombre dérivé : Cette courbe est celle de la fonction cube : f ( x) ? x 3 Faire placer des points M1, M2, M3 ... se rapprochant de A sur la courbe et au crayon les droites correspondantes. On constate qu’on se rapproche de la droite tracée qui est une « position limite ». On nomme cette droite (T) : la repasser en couleur. On remarque que le coefficient directeur de cette droite est 3 qui est le nombre dérivé de f en 1 obtenu au §1.