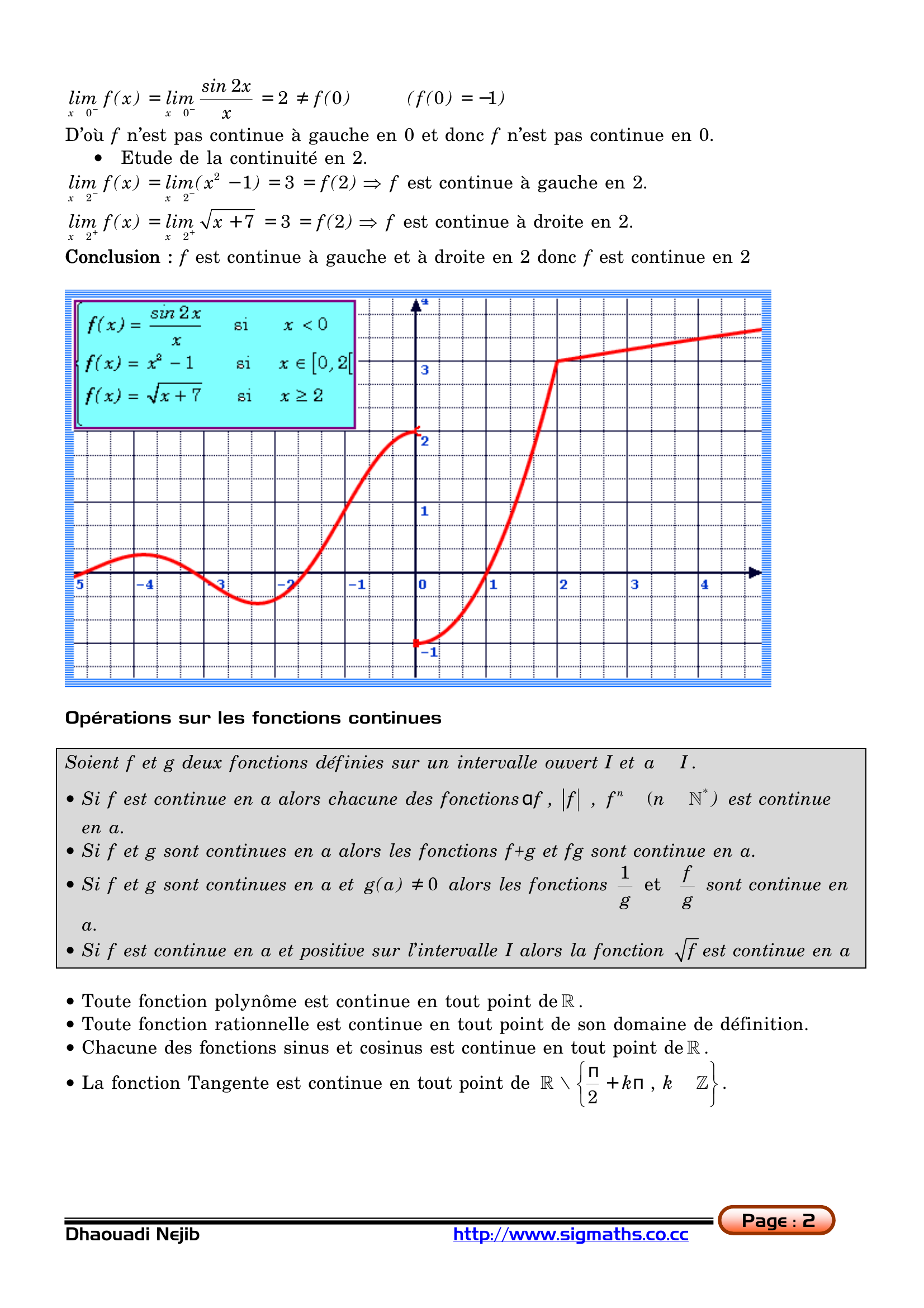
Continuité et limites I. Rappels 1. Continuité Définitions (Rappels) o Soit f une fonction définie sur un intervalle ouvert I et soit a ? I f continue en a si et seulement si lim f(x) = f(a) x->a o Soit f une fonction définie sur un intervalle de la forme [ a, a + ?[ ( ? > 0 ) f est continue à droite en a si et seulement si lim f (x) = f(a) + x->a o Soit f une fonction définie sur un intervalle de la forme ]a - ? , a ] ( ? > 0 ) f est continue à gauche en a si et seulement si lim f(x) = f (a) - x->a Pour étudier la continuité d'une fonction f en un point a il faut que f soit définie en a, à droite de a et à gauche de a Soit f une fonction définie sur un intervalle ouvert I et soit a ? I f continue en a si et seulement si f est continue à droite et à gauche en a Exemples ? x2 - 5 x + 4 ? f ( x) = Soit f la fonction définie sur R par : ? x-1 ? f ( 1 ) = -3 ? Montrons que f est continue en 1. si x?1 x2 - 5x + 4 ( x - 1)( x - 4 ) = lim = lim( x - 4 ) = -3 x ->1 x ->1 x ->1 x ->1 x-1 x-1 lim f ( x) = -3 = f (1) donc f est continue en 1 lim f ( x) = lim x ->1 sin 2x ? ? f ( x) = x ? 2 Soit f la fonction définie par : ? f ( x) = x - 1 ? ? f ( x) = x + 7 ? Etudions la continuité de f en 0 et 2. o Etude de la continuité en 0 Dhaouadi Nejib si x<0 si x ? [ 0, 2[ si x>=2 http://www.sigmaths.co.cc Page : 1 sin 2x = 2 ? f (0) ( f ( 0 ) = -1) x ->0 x ->0 x D'où f n'est pas continue à gauche en 0 et donc f n'est pas continue en 0. o Etude de la continuité en 2. lim f (x ) = lim ( x 2 - 1) = 3 = f ( 2 ) => f est continue à gauche en 2. - - lim f (x ) = lim - - x ->2 x ->2 lim f ( x) = lim + x -> 2+ x ->2 x + 7 = 3 = f ( 2 ) => f est continue à droite en 2. Conclusion Conclusion : f est continue à gauche et à droite en 2 donc f est continue en 2 Opérations sur les fonctions continues Soient f et g deux fonctions définies sur un intervalle ouvert I et a ? I . o Si f est continue en a alors chacune des fonctions ?f , f , f n (n ? N* ) est continue en a. o Si f et g sont continues en a alors les fonctions f+g et fg sont continue en a. 1 f o Si f et g sont continues en a et g(a ) ? 0 alors les fonctions et sont continue en g g a. o Si f est continue en a et positive sur l'intervalle I alors la fonction f est continue en a o Toute fonction polynôme est continue en tout point de R . o Toute fonction rationnelle est continue en tout point de son domaine de définition. o Chacune des fonctions sinus et cosinus est continue en tout point de R . ?? ? o La fonction Tangente est continue en tout point de R \ ? + k? , k ? Z ? . ?2 ? Dhaouadi Nejib http://www.sigmaths.co.cc Page : 2 Prolongement par continuité Soit f une fonction définie sur un intervalle ouvert I, sauf en un réel a de I. Si f admet une limite finie l en a alors la fonction g définie sur I par : g ( x) = f (x ) si x ? a et g(a ) = l est continue en a On dit que f est prolongeable par continuité en a et que g est son prolongement par continuité en a. Exemple 1 - cos( 2x) x2 Montrons que f est prolongeable par continuité en 0. Et pour cela il faut montrer que f admet une limite finie en 0. 1 - cos( 2x ) 1 - cos( 2x) 1 lim f ( x) = lim 4 = lim 4 = 4× = 2 2 2 x ->0 x->0 x ->0 4x 2 ( 2x ) Donc f est prolongeable par continuité en 0 et son prolongement est la fonction g définie 1 - cos( 2x ) sur R par : g( x) = si x ? 0 et g( 0 ) = 2 x2 Continuité sur un intervalle Soit f la fonction définie sur R * par : f ( x) = Une fonction est continue sur un intervalle ouvert si elle est continue en tout point de cet intervalle. Une fonction f est continue sur un intervalle [ a, b] si elle est continue sur ]a, b[ , à droite en a et à gauche en b. De la même façon, on définit la continuité d'une fonction sur les intervalles [ a, b[ , ]a,b] , [a,+?[ et ]-?, a ] Exemple x ? ? f (x ) = Soit la fonction f définie sur [ 0, ?[ par : ? sin x ?f (0 ) = 1 ? Montrons que f est continue sur [ 0, ?[ . si x ? ]0, ?[ o Sur ]0, ?[ , f est le rapport de deux fonctions continues sur ]0, ?[ et dont le dénominateur ne s'annule pas sur cet intervalle donc f est continue sur ]0, ?[ . o A droite en 0, lim f ( x) = lim + + x ->0 x ->0 x 1 1 = lim = = 1 = f ( 0 ) donc f est continue à + sin x x -> 0 sin x 1 x droite en 0. Conclusion : f est continue sur ]0, ?[ et continue à droite en 0 donc f est continue sur [ 0, ?[ . Dhaouadi Nejib http://www.sigmaths.co.cc Page : 3 2. Limites Les résultats résumés dans les tableaux suivants concernent les opérations sur les limites en un réel a, à droite en a, à gauche en a ou à l'infini. Lim f L L L +? -? +? -? Lim g L' +? -? +? -? -? +? Lim f L L?0 ? Lim g L' ? ? Lim( f × g ) LL' ? (RS RS) ? (RS RS) 0 Lim (f+g) L+L' +? -? +? -? ? On On ne peut pas pas conclure On On ne peut pas conclure pas Lim f Lim g L L' ? 0 ? L ? 0 L' ? 0 ? ? 0 f Lim( ) g L L' ? (RS RS) 0 On On ne peut pas pas conclure RS RS : Appliquer la règle des signes