Les symboles mathématiques

Les symboles mathématiques

Symbole Désignation Exemple Énoncé de l’exemple Observations

1. Opérations arithmétiques

+ plus a + 3 a = + 3 a plus trois a égale plus trois 3 est ajouté à la valeur de a le signe + indique une valeur positive

- moins a-3 a = -3 a moins trois a égale moins trois 3 est soustrait de la valeur de a le signe - indique une valeur négative

X multiplié par 5x4 a, b ou ab  8.106  8.10-6 cinq multiplié par quatre a multiplié par b  8 multiplié par 10 à la puissance 6 ou huit, dix puissance six  8 multiplié par 10 à la puissance moins 6 ou huit, dix puissance moins six x ne s’utilise qu’entre deux chiffres le point est généralement omis en algèbre  8.106 = 8x1000000 = 8000000  8.10‘6 = 8x0,000001 =0,000008

/  ou  ou divisé par a/b a : b a  b a divisé par b  a sur b a/b = a:b = sl b  a sur b

2. Égalités, identités, équations, inégalités, inéquations

= égale x=10  y=3x+5 x égale 10 (égalité) le signe = sépare des nombres  ou des expressions qui ont la même valeur connaissant x, on peut calculer y

= identique à (a+b)2=a2+2ab+b2 quelles que soient les valeurs de a et b, (a+b)2 égale a2+2ab+b2

différent de xt 10 x différent de 10 (inégalité) la valeur de x n’est pas égale à 10

3x-8 6 3x - 8 différent de 6 (inéquation)

peu différent de sina « a sinus alpha peu différent de alpha relation vraie pour les faibles valeurs de a

inférieur à 3x« 10 3x inférieur à 10 (inégalité) on disait autrefois inférieur ou égal à

< strictement inférieur à y<2x+7 y strictement inférieur à 2x + 7 (inéquation) on disait autrefois inférieur à ou plus petit que; strictement signifie que l’égalité est exclue

supérieur à 3 s- 3x + 5 3supérieur à 3x + 5 on disait autrefois supérieur ou égal à

> strictement supérieur à a + b > c2 a + b strictement supérieur à c2 on disait autrefois supérieur à ou plus grand que

1 divise ab a divise b b est un multiple de a (par ex. la relation 5 15 est vraie)

3. Autres symboles algébriques

X2 x au carré, x exposant 2, x puissance deux ou x deux 2 est l’exposant de x x2 = x.x

n  en  expo- X3 x au cube, x puissance 3, etc. x3 =x.x.x

puissance x\" x puissance n xn=x.x.... .x (n-1 multiplications)

sant x-n x puissance moins n x-”= l/xn

X1'\" x puissance un sur n x''\" à la puissance n égale x

2y[5 OU (5 racine carrée de 5 ou racine de 5 2/5 = 5,/2 = 2,236;/5x/5 = 5

r racine ’/5 racine cubique de 5 3/5 = 5,/3= 1,710;/5x/5x/5 = 5/5

<5 racine nièm’ de 5 \"/5 = 5,'\"= l,710;/5x/5x...x/5 = 5  (n -1 multiplications)

0 parenthèses (a+b)/(c+d) a+b divisé parc+d l’expression a+b est divisée par l’expression c+d ; chaque couple de parenthèses isole une expression

valeur absolue -15 valeur absolue de -15 -15 = 15 = 15

11 3x+7 valeur absolue de 3x + 7 13x + 71 3s 0 quelle que soit la valeur de x  3x +7 = 3x+7 si 3x+7 > 0  13x + 71 = — (3x + 7) si 3x + 7 < 0

! factorielle 5! factorielle 5 51 = 1x2x3x4x5 = 120  n ! est le produit des n premiers entiers (zéro étant exclu) Symbole Désignation Exemple Énoncé de l’exemple Observations

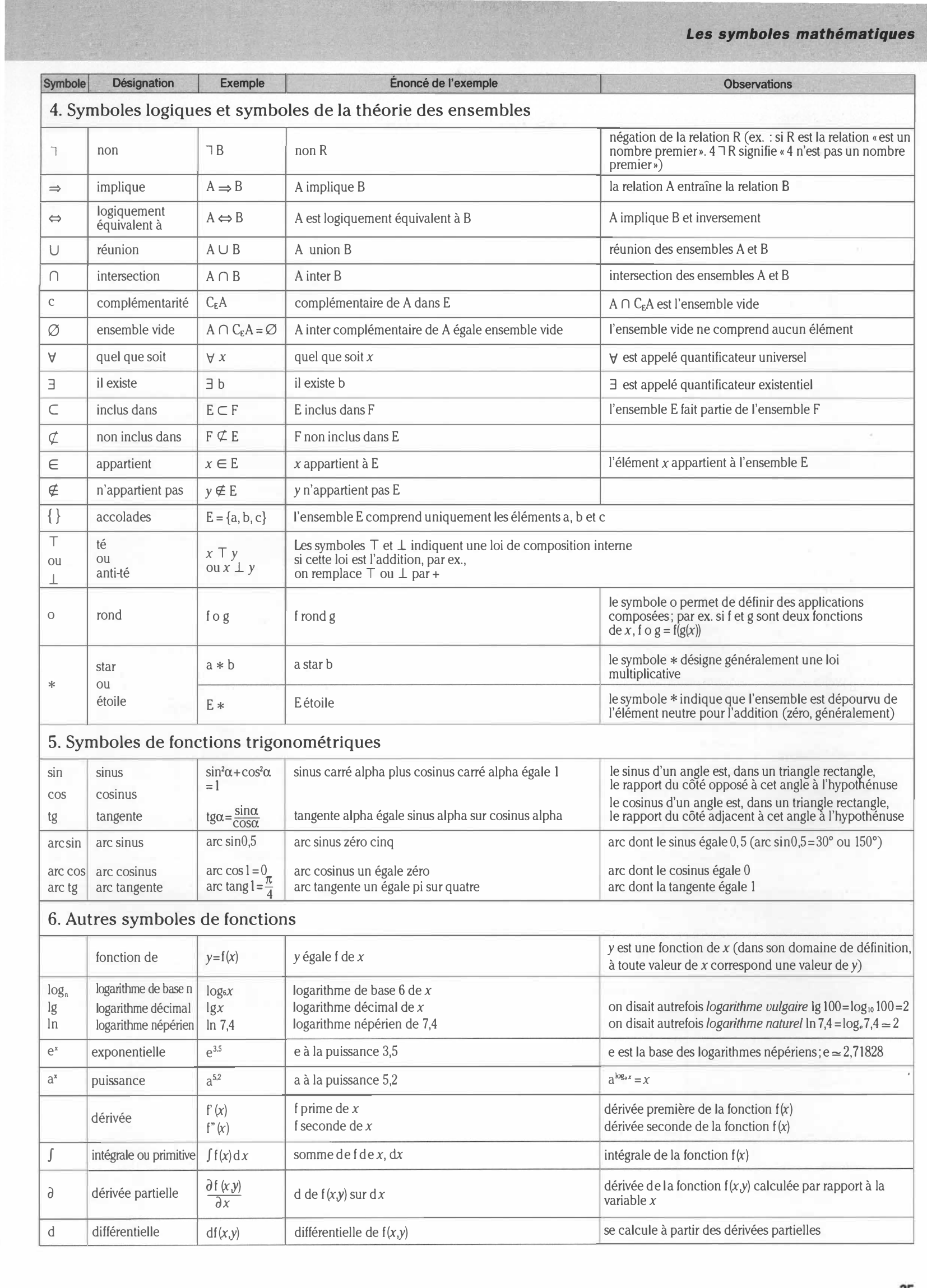
4. Symboles logiques et symboles de la théorie des ensembles

n non AB non R négation de la relation R (ex. : si R est la relation « est un nombre premier». 4 3 R signifie «4 n’est pas un nombre premier»)

=> implique A=>B A implique B la relation A entraîne la relation B

<=> logiquement équivalent à A<=>B A est logiquement équivalent à B A implique B et inversement

U réunion AU B A union B réunion des ensembles A et B

n intersection AA B A inter B intersection des ensembles A et B

c complémentarité cFA complémentaire de A dans E A A CeA est l’ensemble vide

0 ensemble vide AACeA = 0 A inter complémentaire de A égale ensemble vide l’ensemble vide ne comprend aucun élément

V quel que soit VX quel que soit x V est appelé quantificateur universel

3 il existe 3b il existe b 3 est appelé quantificateur existentiel

C inclus dans ECF E inclus dans F l’ensemble E fait partie de l’ensemble F

£ non inclus dans F F non inclus dans E

G appartient xGE x appartient à E l’élément x appartient à l’ensemble E

« n’appartient pas y£E y n’appartient pas E

{} accolades E = {a, b, c} l’ensemble E comprend uniquement les éléments a, b et c

T  ou  1 té ou anti-té x T y oux ± y Les symboles T et 1 indiquent une loi de composition interne si cette loi est l’addition, par ex., on remplace T ou 1 par +

0 rond fog f rond g le symbole o permet de définir des applications composées ; par ex. si f et g sont deux fonctions de x, f o g = f(g(x))

star  OU étoile a * b a star b le symbole * désigne généralement une loi multiplicative

E * E étoile le symbole * indique que l’ensemble est dépourvu de l’élément neutre pour l’addition (zéro, généralement)

5. Symboles de fonctions trigonométriques

sin  cos  tg sinus cosinus tangente sin2a+cos2a = 1  tna=sina  s cosa sinus carré alpha plus cosinus carré alpha égale 1 tangente alpha égale sinus alpha sur cosinus alpha le sinus d’un angle est, dans un triangle rectangle, le rapport du côté opposé à cet angle à l’hypotnénuse le cosinus d’un angle est, dans un triangle rectangle, le rapport du côté adjacent à cet angle a l’hypothénuse

arc sin arc sinus arc sin 0,5 arc sinus zéro cinq arc dont le sinus égale 0,5 (arc sin 0,5=30° ou 150°)

arc cos  arc tg arc cosinus arc tangente arccosl = 0 arctangl = \" arc cosinus un égale zéro  arc tangente un égale pi sur quatre arc dont le cosinus égale 0 arc dont la tangente égale 1

6. Autres symboles de fonctions

fonction de y=f(x) y égale f de x y est une fonction de x (dans son domaine de définition, à toute valeur de x correspond une valeur de y)

log„  1g ln logarithme de base n logarithme décimal logarithme népérien logeX lgx ln 7,4 logarithme de base 6 de x logarithme décimal de x logarithme népérien de 7,4 on disait autrefois logarithme vulgaire 1g 100=loglo 100=2 on disait autrefois logarithme naturel ln 7,4=loge7,4 = 2

ex exponentielle eM e à la puissance 3,5 e est la base des logarithmes népériens ; e=2,71828

ax puissance aM a à la puissance 5,2 akl8,jr=x

dérivée f’M f”(x) f prime de x f seconde dex dérivée première de la fonction f (x) dérivée seconde de la fonction f (x)

J intégrale ou primitive ff(x)dx somme de f de x, dx intégrale de la fonction f(x)

a dérivée partielle dfM dx ddef(x,y)surdx dérivée de la fonction f(x,y) calculée par rapport à la variable x

d différentielle df(x\\y) différentielle de f (x,y) se calcule à partir des dérivées partielles