application - encyclopédie.

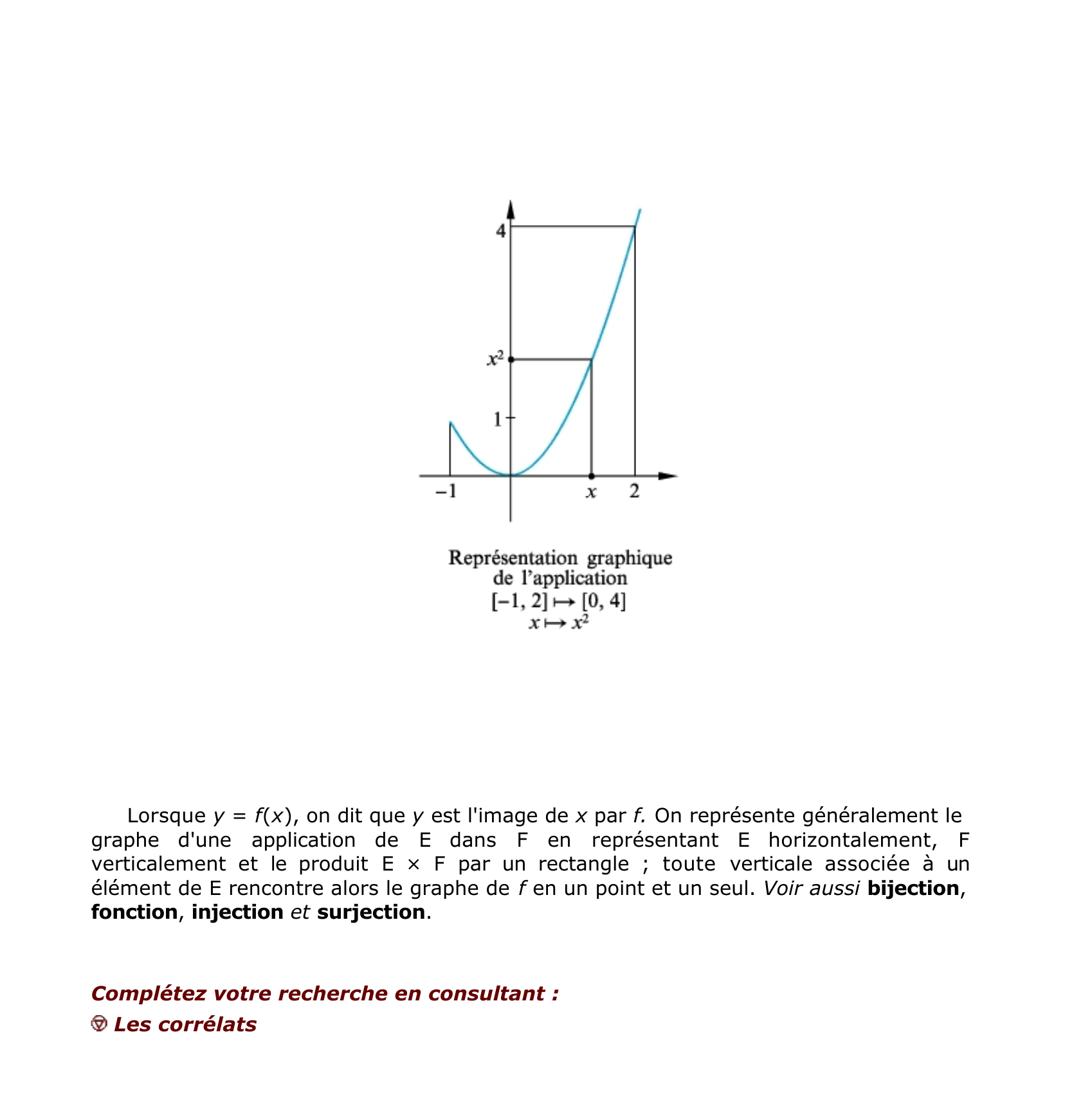
application - encyclopédie. n.f. MATHÉMATIQUES : procédé permettant d'associer tout élément d'un ensemble à un élément bien déterminé d'un autre ensemble. Par exemple, l'application « carré « associe à tout nombre réel x son carré x 2. En fait, une application est une fonction dont on connaît exactement le domaine de définition : par exemple, la fonction « racine carrée « dans u est une application de u+ (ensemble des réels positifs) dans u. Précisément, une application f est définie par la donnée de trois ensembles : un ensemble de départ E ; un ensemble d'arrivée F ; et un ensemble G de couples (x,y), où x m E e t y m F, appelé graphe de f , satisfaisant à la condition suivante : pour tout élément x de E, il existe un élément et un seul y de F tel que (x,y) m G. On note alors f : E ® F x®y et y = f (x). On lit « f est une application de E dans F, qui, à x, fait correspondre y «. Par exemple, si c est l'application « carré «, on écrit : c:u®u x _ x2 2_4 -1_1 1,414... _ 2. Lorsque y = f(x), on dit que y est l'image de x par f. On représente généralement le graphe d'une application de E dans F en représentant E horizontalement, F verticalement et le produit E × F par un rectangle ; toute verticale associée à un élément de E rencontre alors le graphe de f en un point et un seul. Voir aussi bijection, fonction, injection et surjection. Complétez votre recherche en consultant : Les corrélats bijection fonction - 2.MATHÉMATIQUES injection - 3.MATHÉMATIQUES surjection